¿Cuál es la clasificación de los números reales?

Los números reales es el conjunto de números racionales e irracionales que existentes, de los cuales también es posible hallar diversos tipos. Éstos nacieron debido a la necesidad hallada entre los siglos XV y XVII cuando el cálculo no era posible de describir de una manera lógica y precisa, siendo común la utilización de términos o expresiones poco fiables, como por ejemplo “pequeño” o “límite”.

A pesar de que los egipcios ya utilizaban fracciones, no fue hasta la matemática de los griegos en los que se estudió el “número” de una forma más filosófica, donde los seguidores de Pitágoras concluyeron que todo lo de su alrededor son números; y por lo tanto, éstos fueron aplicados en las diferentes áreas.

Clasificación de los números reales según su tipo

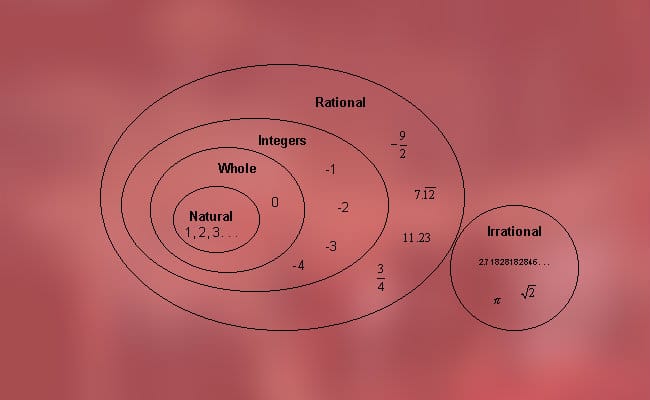
Estos números pueden clasificarse en dos tipos, los cuales mencionábamos anteriormente, es decir, los números racionales (positivos, negativos y cero) e irracionales (algebraicos y trascendentes). De forma más precisa, es posible encontrar la siguiente clasificación:

1. Números racionales

Se denomina así a los números que tienen la capacidad de ser representados como la división de números enteros, o lo que es igual, una fracción común y corriente en la que el numerador y denominador no es cero ni menor a él.

Éstos a su vez también se dividen en varios tipos: enteros (naturales, cero y enteros negativos) y fraccionarios (fracciones propias e impropias).

a) Enteros

Los números enteros son el conjunto de números naturales, enteros negativos y el cero, los cuales son representados por la letra “Z”. Los enteros suelen representarse también en una recta numérica, donde los positivos o naturales están a la derecha, el cero en el medio y los negativos a la izquierda.

• Se considera “números naturales” a aquellos que se utilizan para contar elementos o realizar algunas de las operaciones de cálculo más comunes y sencillas.
• El cero es un valor nulo es decir, carece de alguna cifra significativa cuando no está acompañado. Sin embargo, su posición en un número puede cambiar completamente el significado, ya que cuando está a la derecha del mismo en el que se multiplicaría el valor por diez; mientras que al otro lado no existe modificación.
• Los enteros negativos se utilizan de forma contraria a los positivos o naturales, es decir, en vez de contar, su uso es para restar, deber, gastar o estar por debajo. Para mencionarlos es necesario indicar el término “menos” antes del número, por ejemplo “menos cuatro”.

b) Fraccionarios

También dentro de los números reales es posible hallar este tipo en los racionales, los cuales se originaron con la finalidad de solucionar problemas con respecto a la división de los números naturales. Un número fraccionario es simplemente una expresión que indica la división de una cantidad entre otra.

Las fracciones se caracterizan por posee un numerador y denominador, los cuales están separados entre sí por una barra diagonal u horizontal. Sin embargo, a pesar de que en los enteros también podemos encontrar la “fracción simple”, en este aparatado los tipos de fracciones que encontramos son las propias e impropias.

• Las propias consisten en aquellas donde el numerador es menor que el denominador.
• Las impropias serían lo contrario, es decir, el denominador es mayor que el denominador.

2. Números irracionales

Los irracionales son aquellos números que no tienen la capacidad de ser escritos en una fracción, ya que sus decimales siguen repitiéndose infinitamente. Por ejemplo, es imposible escribir una fracción que incluya el número Pi, e, la razón de oro y raíces cuadradas, cúbicas, entre otras.

Los números irracionales surgieron gracias a la necesidad de un estudiante de Pitágoras de escribir una raíz en forma de fracción; dándose cuenta de que esto no era posible y que se trataba de un número que hoy día conocemos bajo el término de “irracional”. Sin embargo, Pitágoras no estuvo de acuerdo con su descubrimiento, aunque se le atribuye tanto a él como su escuela.

Además, éstos pueden clasificarse en dos tipos, los algebraicos y trascendentes.

• Los algebraicos son aquellos que permiten resolver una ecuación algebraica.
• Los trascendentes son aquellos que no se pueden representar por un número finito de raíces (al contrario de los algebraicos) y que no siguen un patrón en sus decimales. Entre ellos encontramos al número Pi.

Hasta aquí llegamos con la clasificación de números reales, la cual esperamos que haya sido de fácil lectura y entendimiento; ya que muchas personas no son amantes de las matemáticas y hemos hecho todo lo posible por realizar una explicación detallada y sencilla.