Jaká je klasifikace reálných čísel?

L reálná čísla je množina racionálních a iracionálních čísel než existující, z nichž je také možné najít různé typy. Ty se zrodily z důvodu nutnosti, která byla nalezena mezi XV. A XVII. Stoletím, kdy nebylo možné výpočet popsat logickým a přesným způsobem, protože se běžně používaly nespolehlivé výrazy nebo výrazy, například „malý“ nebo „limit“.

Přestože Egypťané již používali zlomky, teprve až v matematice Řeků byla „čísla“ studována filozofičtějším způsobem, kde následovníci Pythagoras usoudili, že vše kolem nich jsou čísla; a proto byly použity v různých oblastech.

Klasifikace reálných čísel podle jejich typu

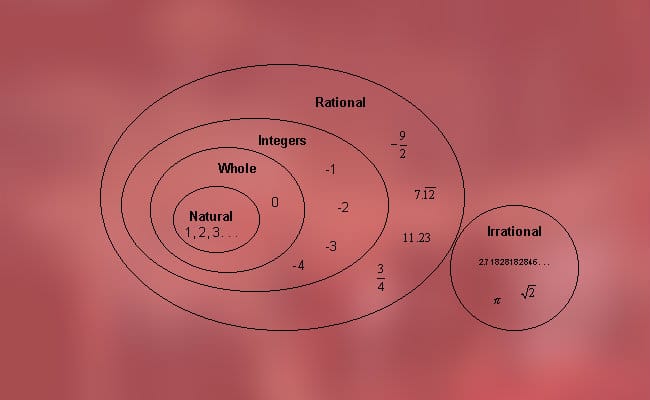
Tato čísla lze rozdělit na dva typy, které jsme zmínili dříve, tj. Racionální čísla (kladná, záporná a nulová) a iracionální (algebraická a transcendentální). Přesněji je možné najít následující klasifikaci:

1. Racionální čísla

Čísla, která mají schopnost být reprezentována jako rozdělení celých čísel, nebo co je stejné, běžný a aktuální zlomek, ve kterém čitatel a jmenovatel nejsou ani nulové, ani menší, než jak se tomu říká.

Ty jsou zase také rozděleny do několika typů: celá čísla (přirozená, nulová a záporná celá čísla) a zlomková (vlastní a nesprávné zlomky).

a) Celá čísla

Celá čísla jsou množinou přirozených čísel, záporných celých čísel a nuly, která jsou reprezentována písmenem „Z“. Celá čísla jsou také obvykle zastoupena na číselné řadě, kde jsou kladné nebo přirozené vpravo, nula uprostřed a záporná vlevo.

• Je považován "přirozená čísla„Pro ty, kteří jsou zvyklí počítat položky nebo provádět některé z běžnějších a nejjednodušších výpočtových operací.
• El cero Je to nulová hodnota, to znamená, že postrádá jakékoli významné číslo, pokud není doprovázeno. Jeho pozice v čísle však může úplně změnit význam, protože když je napravo od něj, ve kterém by vynásobil hodnotu deseti; zatímco na druhé straně není žádná modifikace.
• L záporná celá čísla jsou používány na rozdíl od pozitivního nebo přirozeného, ​​to znamená, že místo počítání slouží k odečítání, dlužení, utrácení nebo být níže. Abychom je zmínili, je nutné před číslem uvést výraz „minus“, například „minus čtyři“.

b) Frakční

Také v reálných číslech je možné tento typ najít v racionálech, které vznikly za účelem řešit problémy týkající se dělení přirozených čísel. Zlomkové číslo je jednoduše výraz, který označuje rozdělení jedné veličiny na druhou.

Frakce se vyznačují tím, že mají čitatele a jmenovatele, které jsou od sebe odděleny úhlopříčkou nebo vodorovnou čarou. Navzdory skutečnosti, že v celých číslech najdeme také „jednoduchý zlomek“, jsou v této části typy zlomků, které najdeme, správné a nesprávné.

• Ty správné se skládají z těch, kde je čitatel menší než jmenovatel.
• Nesprávné by byly opakem, to znamená, že jmenovatel je větší než jmenovatel.

2. Iracionální čísla

Iracionální jsou čísla, která nemají schopnost zápisu zlomkem, protože jejich desetinná místa se neustále opakují. Například je nemožné napsat zlomek, který obsahuje číslo Pi, e, poměr zlata a kořenů čtvercový, kubický, mimo jiné.

Iracionální čísla vznikla díky potřebě studenta Pythagorase napsat kořen jako zlomek; uvědomili jsme si, že to není možné a že to bylo číslo, které dnes známe pod pojmem „iracionální“. Pythagoras však s jeho objevem nesouhlasil, i když je mu připisován stejně jako jeho škole.

Dále je lze rozdělit na dva typy, algebraické a transcendentální.

• L algebraický jsou ty, které umožňují řešení algebraické rovnice.
• L transcendentní Jsou to ty, které nemohou být reprezentovány konečným počtem kořenů (na rozdíl od algebraických) a které nenásledují vzorec na svých desetinných místech. Mezi nimi najdeme číslo Pi.

Zatím přicházíme s klasifikací reálných čísel, která, jak doufáme, byla snadno čitelná a srozumitelná; protože mnoho lidí není milovníkem matematiky a my jsme se snažili poskytnout podrobné a jednoduché vysvětlení.