Wie studiert man ein fünfeckiges Prisma? Ausführliche Erklärung

Es ist eine dreidimensionale geometrische Figur, die aus zwei gleichen parallelen Polygonen als Basis und Seitenflächen besteht, die Parallelogramme sind. Sie erhalten einen bestimmten Namen entsprechend der Anzahl der Seiten, die ihre Basis bilden. So haben wir zum Beispiel, dass wenn seine Basen drei Seiten haben, es ein dreieckiges Prisma, vier rechteckige Seiten, fünf fünfeckige Seiten usw. sein wird.

Das vorliegende Thema ist speziell alles, was damit zu tun hat fünfeckiges PrismaEs ist jedoch notwendig, die gemeinsamen Aspekte von Prismen im Allgemeinen zu kennen.

Allgemeine Eigenschaften eines Prismas

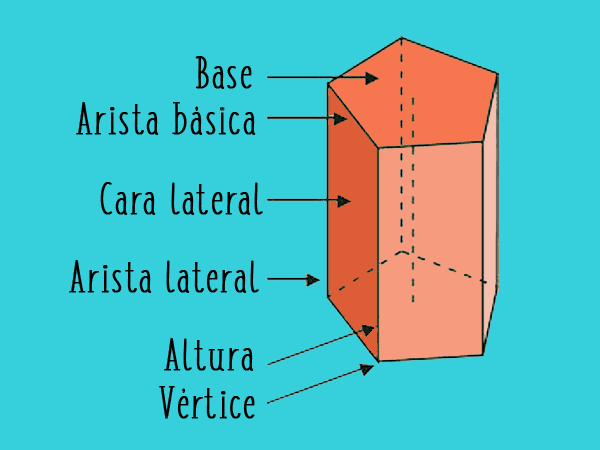
Elemente, aus denen ein Prisma besteht: 

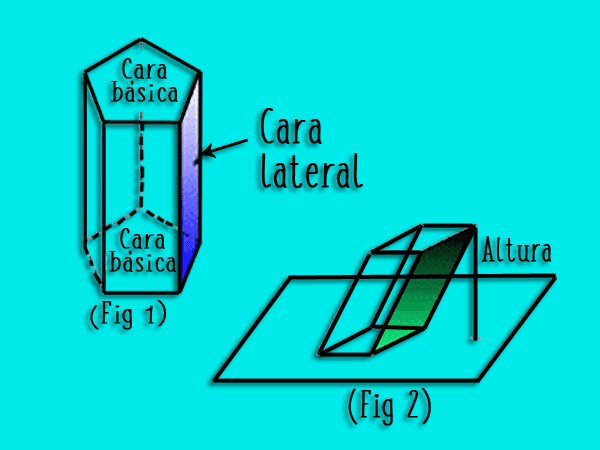
• Bases Sie sind zwei parallele und gleiche Polygone, die den Boden und die Oberseite des Prismas bilden.  Die Anzahl seiner Seiten kann variabel sein und sie sind genau diejenigen, die dem Prisma einen Vor- und Nachnamen geben.
• Seitenflächen: sind die Parallelogramme, die die untere von der oberen Basis trennen 
• Grösse Es ist der Abstand, der die beiden Basen trennt. 
• Kanten: Jede der Seiten der Polygone, die die Basen bilden, wird als Kanten der Basis bezeichnet. Und jede der Seiten der Seitenflächen wird einzeln als Seitenkante bezeichnet.
• Scheitel: Jeder der Punkte, an denen sich die Kanten treffen, wird als Scheitelpunkt bezeichnet.

Klassifizierung von Prismen

Ein Prisma wird nach den Eigenschaften seiner Basen klassifiziert in:

• Regular:Es ist eines, dessen Basis ein Polygon ist, dessen Seiten alle gleich lang sind und dessen Innenwinkel gleich groß sind.
• Irregulär: Es ist eines, dessen Basen durch Polygone mit unterschiedlichen Seiten und Innenwinkeln dargestellt werden.

Entsprechend der Anzahl der Seiten, die ihre Basen haben, werden sie klassifiziert in:

• Dreieckige 3 Seiten
• Viereckige 4 Seiten
• Fünfeckige 5 Seiten
• Sechskant 6 Seiten
• Siebeneckige 7 Seiten
• Achteckige 8 Seiten
• 9-seitiges Eneagon oder Nonagon
• Zehneck 10 Seiten ... und so weiter.

Nach ihren Seitenflächen werden sie eingeteilt in:

• Rechtes Prisma: Es ist dasjenige, das so viele Seitenflächen hat wie seine Basis, sie sind rechteckig und parallel dazu.

• Schräg: Ein schräges Prisma hat keine Rechtwinkligkeit an seinen Seitenflächen in Bezug auf seine Basis. Seine Seitenflächen sind rhomboid. Ihr besonderes Merkmal ist, dass ihre Höhe nicht mit dem Wert ihrer Seitenkanten übereinstimmt.

Nach ihren Innenwinkeln werden sie eingeteilt

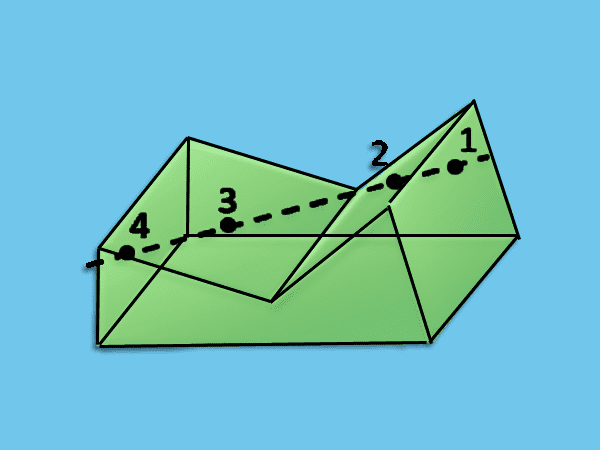
Konkaven: Ein Prisma kann als konkav klassifiziert werden, wenn seine Innenwinkel größer als 180 ° sind. Aufgrund seiner unregelmäßigen Form, die die Sicht eines Schlitzes zur Innenseite des Prismas ergibt, kann es in mehr als einem Punkt geschnitten werden, wenn wir es mit einer geraden Linie kreuzen.

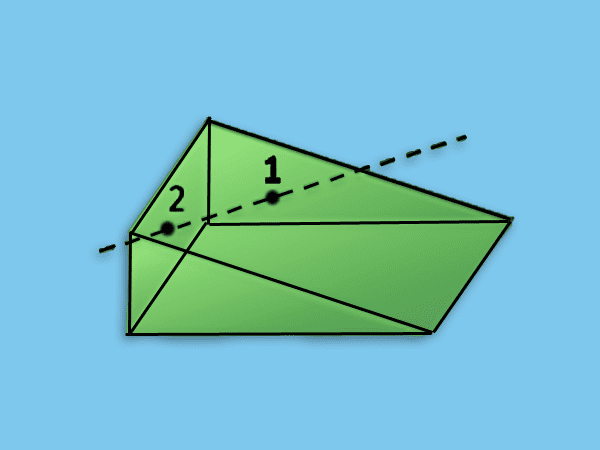
Konvex: Ein Prisma ist konvex, wenn seine Innenwinkel weniger als 180 ° betragen, und andererseits haben wir, dass es beim Kreuzen mit einer Linie nur an zwei eindeutigen Punkten schneidet.

Fünfeckiges Prisma

Jetzt sind wir bereit, mehr über das fünfeckige Prisma zu erfahren. Sobald die Merkmale, die jedem Prisma gemeinsam sind, identifiziert wurden, werden wir uns speziell mit dem fünfeckigen Prisma befassen. Ein fünfeckiges Prisma ist eines, dessen Basis gleiche und parallele Fünfecke und fünf Parallelogramme sind, die seine Seitenflächen bilden.

Beschreibung

Das fünfeckige Prisma weist folgende Eigenschaften auf:

• Bases. Es hat zwei parallele und gleiche Pentagone.
• Faces. Es hat fünf Seitenflächen plus die zwei Basen, insgesamt gibt es sieben Flächen,
• Höhe. Es ist der Abstand zwischen den beiden Basen.
• Scheitel. Sie sind die Punkte des Prismas, an denen drei der Flächen zusammenfallen, insgesamt gibt es 10 Eckpunkte.
• Kanten. Sie sind die Treffpunkte von zwei Flächen des Prismas, insgesamt hat es 15 Kanten.

Nach dem Satz von Euler besteht ein Zusammenhang zwischen der Anzahl der Flächen (C), den Kanten (A) und den Eckpunkten jedes Prismas, dessen Innenwinkel weniger als 180 ° (konvex) betragen.

Unter Anwendung der Formel A = C + V-2 kann die Anzahl der Kanten eines fünfeckigen Prismas ermittelt werden: A = 7 + 10-2 = 15

Wie Berechnen Sie die Fläche eines regulären fünfeckigen Prismas

Die Grundflächen der regelmäßigen Fünfecke und der rechteckigen Seiten sind gleich, sodass die Berechnung der Fläche gegeben ist durch:

Fläche = 5. L. (ap. + H), wobei L das Maß für eine der Seiten des Fünfecks ist, ap. (Apothem) ist der kürzeste Abstand von der Mitte zu beiden Seiten und h ist die Höhe des Prismas.

Wie finde ich den Wert von ap (Apothem) eines fünfeckigen Prismas?

Es ist eine Variable, die wir nicht so offensichtlich kennen wie die anderen. Nun, hier ist die mathematische Formel, um es zu finden.

Wenn Sie die Anzahl der Seiten (N) und ihr Maß (L) kennen, berechnen Sie zunächst den zentralen Winkel, der zwischen der Mitte des Polygons und zwei aufeinander folgenden Scheitelpunkten gebildet wird:

? = 360 ° / N.  

Beispiel: zentraler Winkel eines Fünfecks? = 360 ° / 5 entspricht 72 °.

Als nächstes kommt das Apothem

Teilen Sie das Maß einer der Seiten (L) durch die doppelte Tangente der Hälfte des Mittelwinkels (?).

ap = L / 2 x Tang (? / 2)

Beispiel: Wenn Sie ein fünfeckiges Prisma haben, dessen Seiten ein Maß von 20 cm und eine Höhe von 30 Zentimetern haben, lassen Sie uns seine Fläche finden. Wir wissen bereits, dass der Wert des Mittelwinkels eines regulären Fünfecks 72 ° beträgt. Lassen Sie uns sein Apothem finden:

Ap = 20/2 x Tang (72/2)

Ap = 20/2 x Tang (36)

Ap = 20/2 x (0.73)

Ap = 20 / 1.46

Ap = 13,69 cm.

Nun ja, wir haben alle Daten, um Ihre Region zu bestimmen:

Fläche = 5 x L x (ap + h)

5 x 20 (13,69 + 30)

100 (43,69)

Fläche = 4369 cm.

Bereich eines unregelmäßigen fünfeckigen Prismas

Unter Berücksichtigung, dass ein unregelmäßiges fünfeckiges Prisma zwei unregelmäßige Fünfecke als Basis hat, ist es notwendig, die Fläche des unregelmäßigen Fünfecks (Ab), seinen Umfang (Pb) und die Höhe des Prismas zu finden, um später die Fläche von zu berechnen Das Prisma.

Die Formel für die Fläche eines unregelmäßigen fünfeckigen rechten Prismas lautet:

Prismenfläche = 2. Ab + Pb. h

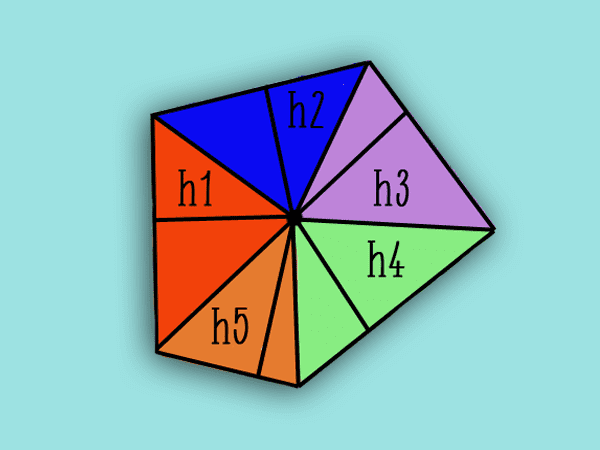
Der Bereich des unregelmäßigen Fünfecks der Basis (Ab) wird durch die gefunden Methode von TriangulationDies bedeutet, dass es in kleinere dreieckige Figuren unterteilt wird, um ihre Flächen zu berechnen, und somit die Gesamtfläche des Fünfecks leichter erhalten wird, indem alle addiert werden.

Der Umfang einer unregelmäßigen Fünfeckbasis (Pb) Es wird durch Hinzufügen des Maßes seiner fünf Seiten gefunden.

Bereich eines schrägen fünfeckigen Prismas

Die Flächenberechnungsformel für diese Art von Prisma unterscheidet sich von der des rechten fünfeckigen Prismas.

Die Fläche der Basen wird auf die gleiche Weise wie in der Geraden berechnet, der Unterschied liegt in den Seiten aufgrund der Tatsache, dass sie geneigt sind.

Die Fläche einer der Seiten eines schrägen fünfeckigen Prismas wird basierend auf der Messung einer Seitenkante und des Umfangs des berechnet Prisma gerader Abschnitt.

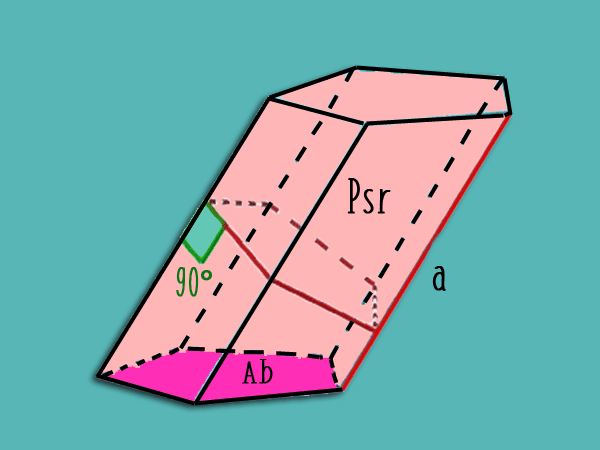
Der Schnittpunkt einer Ebene mit dem Prisma in einem Winkel von 90 ° zu jeder der Seitenkanten ist der gerade Abschnitt des Prismas. Das heißt, es ist die flache Basis, die beobachtet wird, wenn das Prisma quer geteilt wird.

So finden Sie die grafische Darstellung der gerader Abschnitt eines schrägen Prismas Platzieren Sie das Quadrat auf einer seiner Kanten und zeichnen Sie unter Bildung eines 90 ° -Winkels eine Linie, die die benachbarte Kante erreicht, und so weiter mit den anderen Kanten. Sobald dieser Vorgang abgeschlossen ist, kann diese Oberfläche in der Ebene sichtbar gemacht werden.

Fläche = 2. Ab + Psr. zu  

Wo  Ab ist der Bereich der Basis, psr ist der Umfang des geraden Abschnitts des Prismas und a eine Seitenkante.

Um den Wert des Umfangs des geraden Abschnitts zu bestimmen, reicht es aus, eine seiner Kanten in einem Winkel von 90 ° zu quadrieren, den Abstand von dieser Kante zu der Stelle zu messen, an der sie ihre parallele Kante schneidet, und sie fünfmal hinzuzufügen.

Volumen eines fünfeckigen Prismas

Um das Volumen eines fünfeckigen Prismas zu berechnen, sowohl gerade als auch schräg, wird die allgemeine Formel für alle Arten von Prisma angewendet: Multiplizieren Sie die Fläche der Basis (Ab) mit der Höhenmessung (h).

Volumen = Ab. h

Wenn wir Ab durch eine eigene Formel ersetzen, haben wir Volumen = 5. L. ap / 2. h

Denken Sie daran, dass bei einem rechten Prisma die Höhenmessung gleich der Seitenkantenmessung ist während in einem schrägen Prisma Die Höhe des Prismas stimmt nicht mit der Messung der Seitenkante überein, unabhängig von der Art des Prismas. Achten Sie darauf, nicht zu verwechseln.

Wie man ein gerades regelmäßiges fünfeckiges Prisma macht

? = 108 ° Innenwinkel zwischen zwei Seiten des Basis-Fünfecks (festes Maß für eine fünfeckige Figur)

L = Seite

H = Höhe

Fünfeckiger Basishub

Bevor mit dem Zeichnen des Prismas begonnen wird, müssen seine Basen definiert werden. Auf einfache und nicht so technische Weise werde ich erklären, wie man eine normale fünfeckige Figur macht.

• Zeichnen Sie eine gerade Linie, die als Ausgangspunkt dient (Abb. 1).
• Markieren Sie das Maß, das Sie an den Seiten Ihres Fünfecks geben möchten, Linie (ab) Abb. 2
• Mit Hilfe eines Winkelmessers an der Stelle anhalten “a "Und suchen Sie links nach dem Winkel von 108 °, zeichnen Sie eine Linie zwischen" a "und dem Schnittpunkt mit dem gefundenen Winkel und markieren Sie darauf das für die Seiten des Fünfecks gewählte Maß. (Linie ac) Abb. 3
• Lehnen Sie sich auf Punkt b rechts Gehen Sie genauso vor wie oben und suchen Sie die andere Seite (Zeile bd) Abb. 4
• Dann stützen Sie sich auf Punkt "c", achten Sie immer auf einen Winkel von 108 ° und zeichnen Sie die (ce-Linie) Abb.5
• Verbinden Sie schließlich die ed-Punkte, aus denen die fehlende Seite besteht. Es sollte automatisch einen Winkel von 108 ° haben. Abb. 6

Diese geometrische Figur hat technischere und präzisere Formen für ihren Strich, aber hier erkläre ich es Ihnen auf einfache Weise, indem ich nur Lineale und / oder Quadrate und einen Winkelmesser verwende.

Der Erfolg des Aufbaus Ihres Prismas hängt von der Genauigkeit der Verfolgung seiner Basen ab.

Und die Genauigkeit bei der Konstruktion Ihrer fünfeckigen Basis hängt von Ihren Fähigkeiten und Kenntnissen der von mir vorgeschlagenen Messinstrumente ab.

Prismenspur

• Zeichnen Sie eine lange gerade Linie, die als Basis für den Beginn des Strichs dient.
• Markieren Sie in dieser Zeile die Messung (L) fünfmal nacheinander.
• Zeichnen Sie senkrecht zu jedem Punkt die vertikalen Linien, die die Kanten darstellen, mit dem Maß für (h) Höhe.
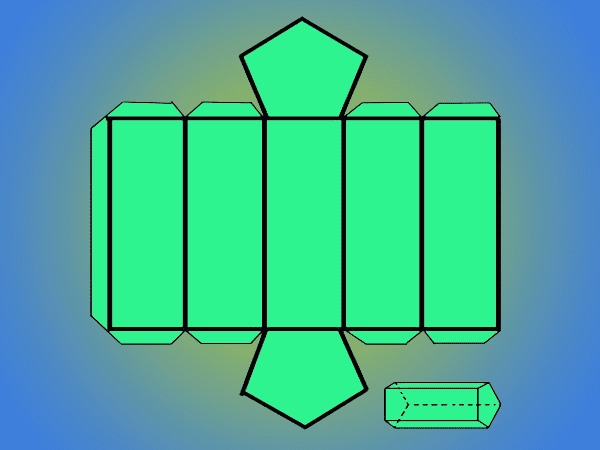
• Verbinden Sie alle Punkte mit einer geraden Linie, und Sie erhalten ein Rechteck, das in fünf gleiche und parallele Abschnitte unterteilt ist. Diese repräsentieren jede der Seitenflächen des Prismas.
• Zeichnen oder fügen Sie auf dem Rechteck oder der Mittelfläche oder der von Ihnen bevorzugten Fläche die fünfeckige Basis sowohl oben als auch unten hinzu. Es ist notwendig, dass Sie es zuerst tun und basierend darauf das Prisma zeichnen.
• Fügen Sie Registerkarten auf allen Seiten der Seitenflächen hinzu, mit Ausnahme einer davon. Diese Registerkarten helfen Ihnen beim Zusammenbau des Prismas.
• Schneiden Sie die Wimpern ab und tragen Sie Klebstoff auf, markieren Sie alle Linien, um eine kleine Pause zu erzielen, und erleichtern Sie das Biegen der Kanten.