What is the classification of the real numbers?

The real numbers is set of rational and irrational numbers than existing, of which it is also possible to find various types. These were born due to the necessity found between the XV and XVII centuries when the calculation was not possible to describe in a logical and precise way, being common the use of unreliable terms or expressions, such as "small" or "limit".

Although the Egyptians already used fractions, it was not until the mathematics of the Greeks in which the "number" was studied in a more philosophical way, where the followers of Pythagoras concluded that everything around them is numbers; and therefore, these were applied in the different areas.

Classification of real numbers according to their type

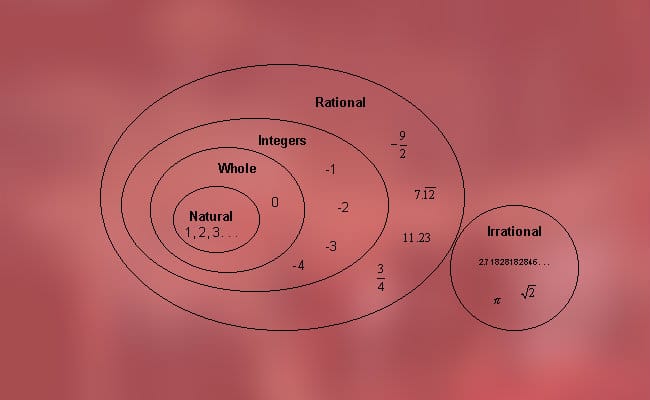
These numbers can be classified into two types, which we mentioned earlier, that is, rational numbers (positive, negative and zero) and irrational (algebraic and transcendental). More precisely, it is possible to find the following classification:

1. Rational numbers

Numbers that have the ability to be represented as the division of whole numbers, or what is the same, a common and current fraction in which the numerator and denominator are neither zero nor less than it is called this way.

These in turn are also divided into several types: integers (natural, zero and negative integers) and fractional (proper and improper fractions).

a) Integers

The integers are the set of natural numbers, negative integers and zero, which are represented by the letter "Z". The integers are also usually represented on a number line, where the positive or natural ones are on the right, the zero in the middle and the negative ones on the left.

• Is considered "natural numbers”To those who are used to count items or perform some of the more common and simple calculation operations.
• El zero It is a null value, that is, it lacks any significant figure when it is not accompanied. However, its position in a number can completely change the meaning, since when it is to the right of it in which it would multiply the value by ten; while on the other side there is no modification.
• The negative integers they are used contrary to the positive or natural, that is, instead of counting, their use is to subtract, owe, spend or be below. To mention them, it is necessary to indicate the term "minus" before the number, for example "minus four".

b) Fractional

Also within the real numbers it is possible to find this type in the rationals, which originated with the purpose of solve problems regarding the division of natural numbers. A fractional number is simply an expression that indicates the division of one quantity by another.

Fractions are characterized by having a numerator and denominator, which are separated from each other by a diagonal or horizontal bar. However, despite the fact that in the integers we can also find the “simple fraction”, in this section the types of fractions that we find are proper and improper.

• The proper ones consist of those where the numerator is less than the denominator.
• The improper ones would be the opposite, that is, the denominator is greater than the denominator.

2. Irrational numbers

Irrationals are those numbers that do not have the ability to be written in a fraction, since their decimals continue to repeat themselves infinitely. For example, it is impossible to write a fraction that includes the number Pi, e, the ratio of gold and roots square, cubic, among others.

Irrational numbers arose thanks to the need of a student of Pythagoras to write a root as a fraction; realizing that this was not possible and that it was a number that we know today under the term "irrational". However, Pythagoras disagreed with his discovery, although it is attributed as much to him as his school.

Furthermore, these can be classified into two types, algebraic and transcendental.

• The algebraic are those that allow solving an algebraic equation.
• The transcendent They are those that cannot be represented by a finite number of roots (unlike the algebraic ones) and that do not follow a pattern in their decimals. Among them we find the number Pi.

So far we come with the classification of real numbers, which we hope has been easy to read and understand; since many people are not lovers of mathematics and we have done our best to provide a detailed and simple explanation.