Quelle est la classification des nombres réels?

Les nombres réels est le ensemble de nombres rationnels et irrationnels qu'existant, dont il est également possible de trouver différents types. Celles-ci sont nées en raison de la nécessité trouvée entre les XVe et XVIIe siècles lorsque le calcul n'était pas possible de décrire de manière logique et précise, étant courant l'utilisation de termes ou d'expressions peu fiables, tels que «petit» ou «limite».

Bien que les Égyptiens utilisaient déjà des fractions, il a fallu attendre les mathématiques des Grecs pour étudier le «nombre» d'une manière plus philosophique, où les adeptes de Pythagore ont conclu que tout autour d'eux est des nombres; et donc, ceux-ci ont été appliqués dans les différents domaines.

Classification des nombres réels selon leur type

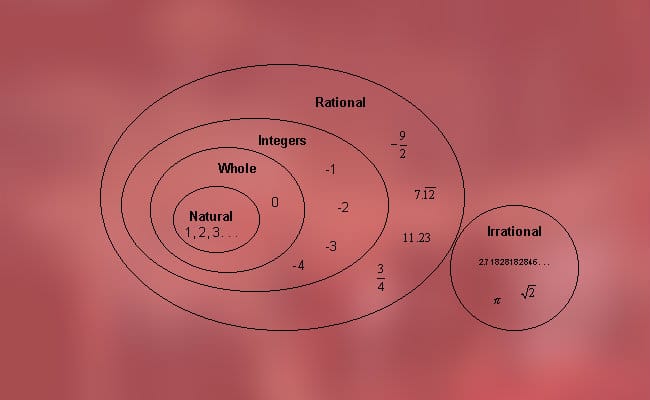
Ces nombres peuvent être classés en deux types, que nous avons mentionnés précédemment, à savoir les nombres rationnels (positifs, négatifs et nuls) et irrationnels (algébriques et transcendantaux). Plus précisément, il est possible de retrouver la classification suivante:

1. Nombres rationnels

Les nombres qui ont la capacité d'être représentés comme la division de nombres entiers, ou ce qui est la même chose, une fraction courante et courante dans laquelle le numérateur et le dénominateur ne sont ni nuls ni inférieurs à ce qu'il est appelé ainsi.

Ceux-ci à leur tour sont également divisés en plusieurs types: entiers (entiers naturels, nuls et négatifs) et fractionnaires (fractions propres et impropres).

a) Entiers

Les entiers sont l'ensemble des nombres naturels, des entiers négatifs et zéro, qui sont représentés par la lettre "Z". Les entiers sont également généralement représentés sur une droite numérique, où les positifs ou naturels sont à droite, le zéro au milieu et les négatifs à gauche.

• Est considéré "nombres naturels»À ceux qui ont l'habitude de compter des éléments ou d'effectuer certaines des opérations de calcul les plus courantes et les plus simples.
• El cero Il s'agit d'une valeur nulle, c'est-à-dire qu'il ne lui manque aucun chiffre significatif lorsqu'il n'est pas accompagné. Cependant, sa position dans un nombre peut changer complètement le sens, puisque quand elle est à sa droite dans laquelle elle multiplierait la valeur par dix; tandis que de l'autre côté il n'y a aucune modification.
• Les entiers négatifs Ils sont utilisés contrairement au positif ou au naturel, c'est-à-dire qu'au lieu de compter, leur usage est de soustraire, de devoir, de dépenser ou d'être en dessous. Pour les mentionner, il faut indiquer le terme «moins» avant le nombre, par exemple «moins quatre».

b) Fractionnel

Aussi dans les nombres réels, il est possible de trouver ce type dans les rationnels, qui ont été créés dans le but de résoudre des problèmes concernant la division des nombres naturels. Un nombre fractionnaire est simplement une expression qui indique la division d'une quantité par une autre.

Les fractions sont caractérisées en ce qu'elles ont un numérateur et un dénominateur, qui sont séparés l'un de l'autre par une barre diagonale ou horizontale. Cependant, malgré le fait que dans les entiers, nous pouvons également trouver la «fraction simple», dans cette section, les types de fractions que nous trouvons sont corrects et impropres.

• Les bons sont ceux où le numérateur est inférieur au dénominateur.
• Les impropres seraient le contraire, c'est-à-dire que le dénominateur est plus grand que le dénominateur.

2. Nombres irrationnels

Les irrationnels sont ces nombres qui n'ont pas la capacité d'être écrits en fraction, puisque leurs décimales continuent à se répéter à l'infini. Par exemple, il est impossible d'écrire une fraction qui inclut le nombre Pi, e, le rapport de l'or et des racines carré, cubique, entre autres.

Les nombres irrationnels sont apparus grâce à la nécessité pour un étudiant de Pythagore d'écrire une racine sous forme de fraction; se rendant compte que ce n'était pas possible et que c'était un nombre que nous connaissons aujourd'hui sous le terme «irrationnel». Cependant, Pythagore n'était pas d'accord avec sa découverte, bien qu'elle lui soit autant attribuée que son école.

De plus, ceux-ci peuvent être classés en deux types, algébriques et transcendantaux.

• Les algébrique sont ceux qui permettent de résoudre une équation algébrique.
• Les transcendant Ce sont celles qui ne peuvent pas être représentées par un nombre fini de racines (contrairement aux racines algébriques) et qui ne suivent pas un modèle dans leurs décimales. Parmi eux, nous trouvons le nombre Pi.

Jusqu'à présent, nous arrivons à la classification des nombres réels, qui, nous l'espérons, a été facile à lire et à comprendre; car beaucoup de gens ne sont pas amateurs de mathématiques et nous avons fait de notre mieux pour fournir une explication détaillée et simple.