ચાલો આપણે જાણીએ તમામ પ્રકારના ગણિત કાર્યો, બંને વિદ્યાર્થીઓ અને વૈજ્ .ાનિક શાખાના પ્રેમીઓ માટે કંઈક આવશ્યક છે, જેથી તેઓને તેમના જ્ knowledgeાનમાં આગળ વધવાનું ચાલુ રાખવા માટે એક આવશ્યક આધાર મળશે.
ગાણિતિક કાર્યો શું છે
ફંક્શન એ બે સેટ અથવા માત્રા વચ્ચેનો સંબંધ એવી રીતે છે કે પ્રથમ અને બીજા વચ્ચે કિંમતોની સમાનતા સ્થાપિત થાય છે.
આપણે કોઈ ગ્રાફિકલી રીતે ફંક્શનનું પ્રતિનિધિત્વ કરી શકીએ છીએ જેથી અમે બંને પરિમાણો વચ્ચેના સંબંધને અવલોકન કરી શકીએ, જે તેની સમજને સરળ બનાવે છે અને આપણે ખરેખર જેની ગણતરી કરીએ છીએ તે જાણવા આપણા મનને ખોલે છે.
યાદ રાખો કે ગણિત ખૂબ જ સુંદર હોઈ શકે છે, પરંતુ ફક્ત જો આપણે પ્રક્રિયાઓ અને ઉદ્દેશો સમજીશું, કારણ કે, જો આપણી પાસે સારો આધાર નથી અને માત્ર ગણતરી પર ધ્યાન કેન્દ્રિત કર્યું છે, તો અંતે તે એક વિષય બનશે જે ખૂબ જ ચ upાવ પર કરવામાં આવે છે. . તેથી તે આવશ્યક છે કે વિધેયોની ગણતરી કરવા ઉપરાંત, તમે તેમના અર્થના વિશ્લેષણ માટે થોડો સમય પસાર કરો અને, આ માટે, તમે જે શ્રેષ્ઠ કરી શકો તે ગ્રાફિકલી રીતે તેમનું પ્રતિનિધિત્વ કરવું.
તમામ પ્રકારના ગણિતના કાર્યો
એકવાર આપણે કોઈ ફંક્શનની કલ્પના સમજીએ, તો આપણે આજે અસ્તિત્વમાં છે તેવા તમામ પ્રકારના ગાણિતિક કાર્યોનું વિશ્લેષણ આગળ ધપાવી શકીએ.
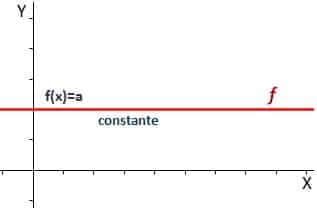
સતત કાર્ય
ઉના સતત કાર્ય તે એક છે જેમાં આપણે ફક્ત કહ્યું કાર્ય માટે જ એક પરિણામ છે, જેથી આપણે નીચેની છબીમાં જે જોઈ શકીએ તેવું જ કંઈક મેળવીએ, એટલે કે, આડી લીટી:
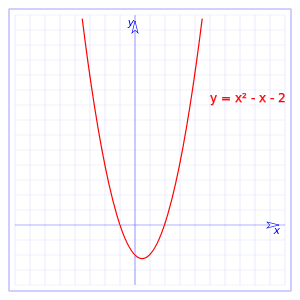
ચતુર્થાત્મક કાર્ય
ઉના વર્ગાત્મક કાર્ય પ્રકારનું કાર્ય છે f (x) = ax2 + bx + c, જેથી કોઈ પણ સંજોગોમાં શૂન્યથી અલગ હોવાને કારણે એ, બી અને સી સ્થિરતા હશે. આ રીતે, જે પ્રાપ્ત થાય છે તે એક પરબlaલા છે જે ખુલ્લા અથવા નીચે થઈ શકે છે, તેના પર આધાર રાખીને કે કોઈનું મૂલ્ય શૂન્ય કરતા વધારે છે, અથવા જો તેની કિંમત શૂન્યથી ઓછી છે. જો તે ઉચ્ચ મૂલ્ય છે, તો તે ઉપર તરફ ખુલશે, અને જો તે શૂન્યથી ઓછું હોય, તો તે નીચે તરફ ખુલશે.
તે નોંધવું જોઈએ કે ચતુર્ભુજ કાર્યો બહુકોણ કાર્યો છે.
રેખીય કાર્ય
La રેખીય મસ્તી આકાર ધરાવે છે તે એક છે f (x) = mx + b, જ્યાં એમ તે છે જે theાળ અમને કહે છે, જ્યારે b એ વાયનું મૂલ્ય છે, જેથી સીધી રેખા મળે પરંતુ આ સમયે કોઈ ચોક્કસ ઝોક અથવા opeાળ સાથે.
તેના પર ધ્યાન આપવું મહત્વપૂર્ણ છે રેખીય કાર્ય એ બહુપદી કાર્ય છે, એક પ્રકારનું ફંક્શન કે જેના વિશે આપણે નીચે શીખીશું.
બહુપદી કાર્ય
આ માટે બહુપદી કાર્ય, તે વાસ્તવિક સંખ્યાઓ અને સકારાત્મક પૂર્ણાંક એક્સ્પ્નોન્ટ્સ સાથેનું એક કાર્ય છે. એ નોંધવું જોઇએ કે તમામ બહુપદી કાર્યોનું ડોમેન વાસ્તવિક સંખ્યાઓનો સમૂહ છે.
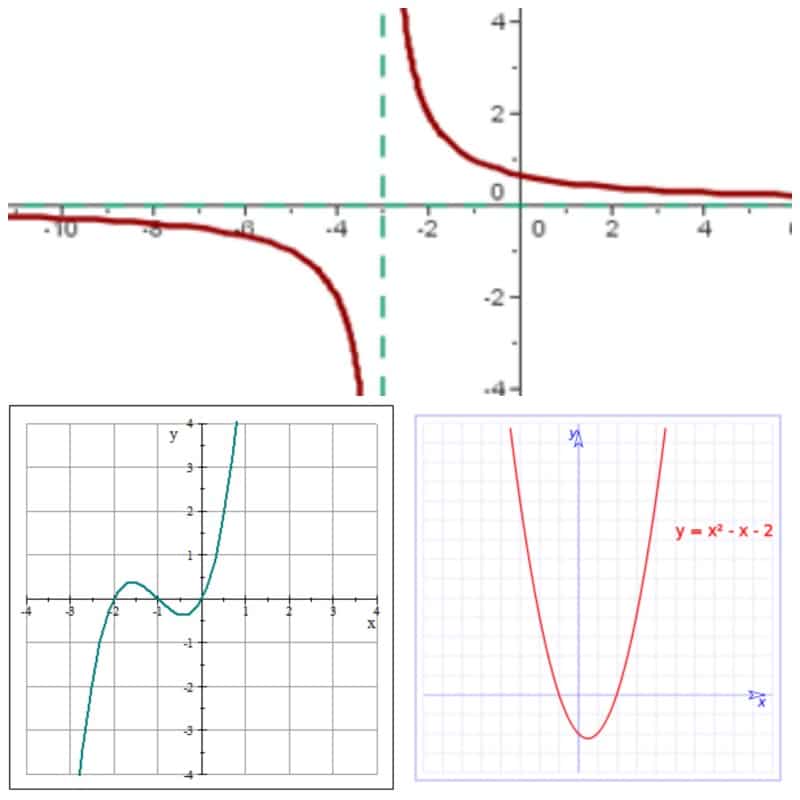
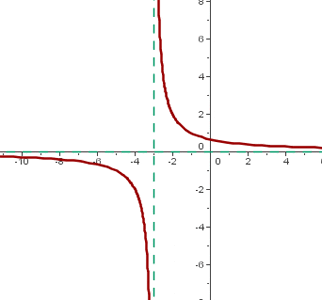
તર્કસંગત કાર્ય
છેવટે અમારી પાસે તર્કસંગત કાર્ય જે બે બહુમુખી કાર્યોના પરિણામી ભાગ છે, જેથી તે સ્થાપિત થાય ક્યૂ (એક્સ) = એફ (એક્સ) / જી (એક્સ).
ધ્યાનમાં રાખવાની એક વિગત એ છે કે બહુપદી કાર્યની ડોમેન વાસ્તવિક સંખ્યાઓ મેળવે છે.
લાઇનનું કાર્ય
જ્યારે આપણે એફેઇન ફંક્શન વિશે વાત કરીશું, ત્યારે આપણે તેનો ઉલ્લેખ કરવો પડશે તે બહુપદી કાર્ય છે. તે પણ આપણે ગાણિતિક કાર્યોની સૂચિમાં તેનો ઉલ્લેખ કર્યો છે. તેથી, એફેનમાં પાછા ફરતા, તે એક તરીકે વ્યાખ્યાયિત કરવામાં આવે છે જે કોઓર્ડિનેટ્સના મૂળથી પસાર થતું નથી, એટલે કે, 0,0 બિંદુને સ્પર્શતું નથી. તે લીટીઓ છે જે નીચેના સૂત્ર દ્વારા સંચાલિત છે:
એફ (એક્સ) = એમએક્સ + એન
એમ theાળ હશે, એટલે કે, એક્સ અક્ષ અથવા એબ્સિસિસાના સંદર્ભમાં વલણ. જ્યારે તે સકારાત્મક હોય છે, ત્યારે ફંક્શન વધતું હોવાનું કહેવાય છે. તેથી જો તે નકારાત્મક છે, તો તે ઘટતું જશે. N એ ગોઠવણ કરશે, બિંદુ જ્યાં રેખા સંકલન અક્ષને કાપી નાખશે.
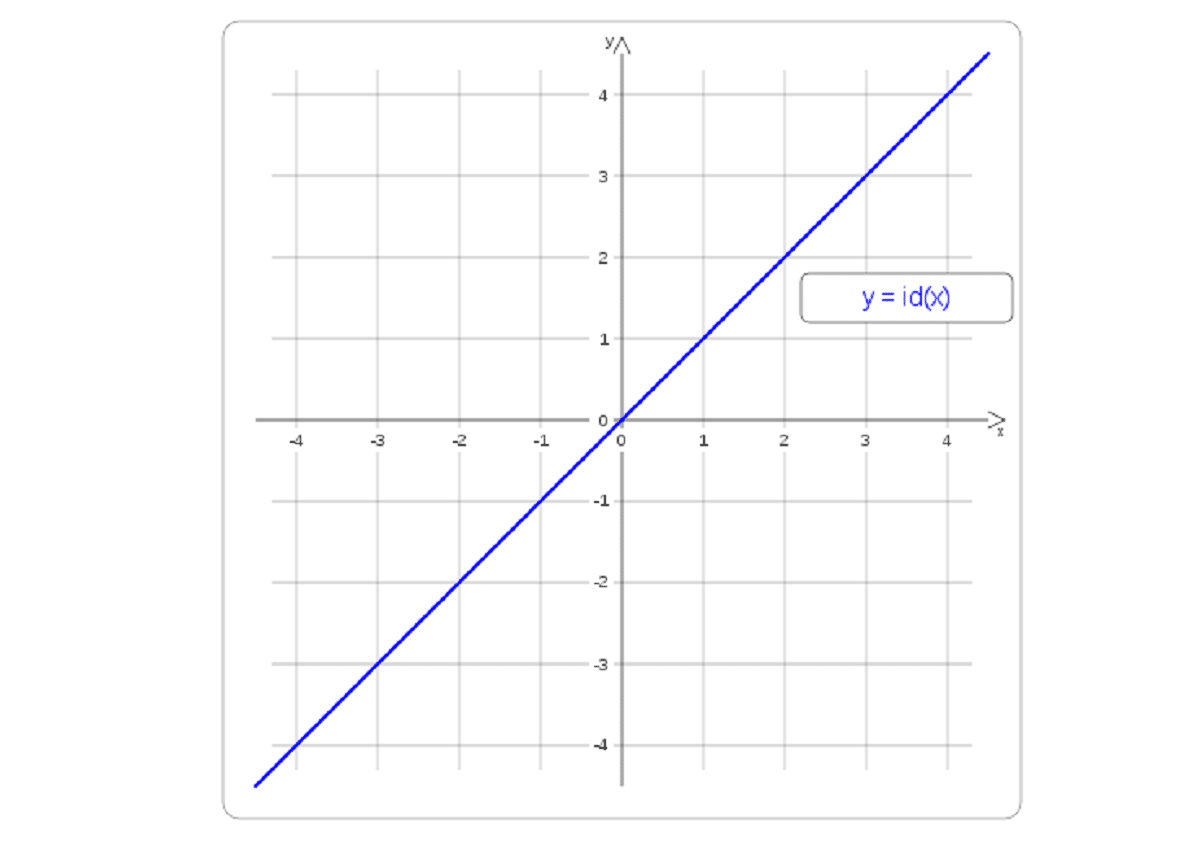
ઓળખ કાર્ય
તે એક સેટ પોતે જ કાર્ય કરે છે. એટલે કે, કોઈપણ પ્રકારના તત્વની છબી સમાન હશે. આપણે તેને સામાન્ય રીતે આઈ.ડી. જ્યારે આપણે કોઈ ઓળખાણ ફંક્શનની વાત કરીએ છીએ ત્યારે આપણે રેખીય ફંક્શનની પણ વાત કરીએ છીએ, જ્યાં m 1 ની બરાબર છે અને સંકલન અક્ષ દ્વારા પસાર થાય છે. આનો અર્થ એ કે તે પ્રથમ અને ત્રીજા ચતુર્થાંશ અને બંનેને સમાન ભાગોમાં વહેંચશે. યાદ રાખો કે આઈડી હંમેશાં તટસ્થ તત્વ હશે
આઈડી આર: આર - આર
ID r (x): = x
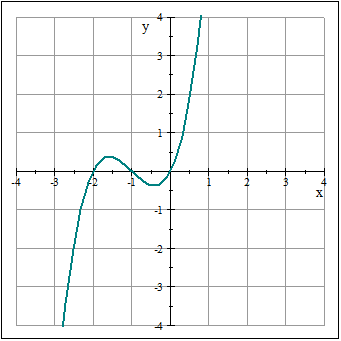
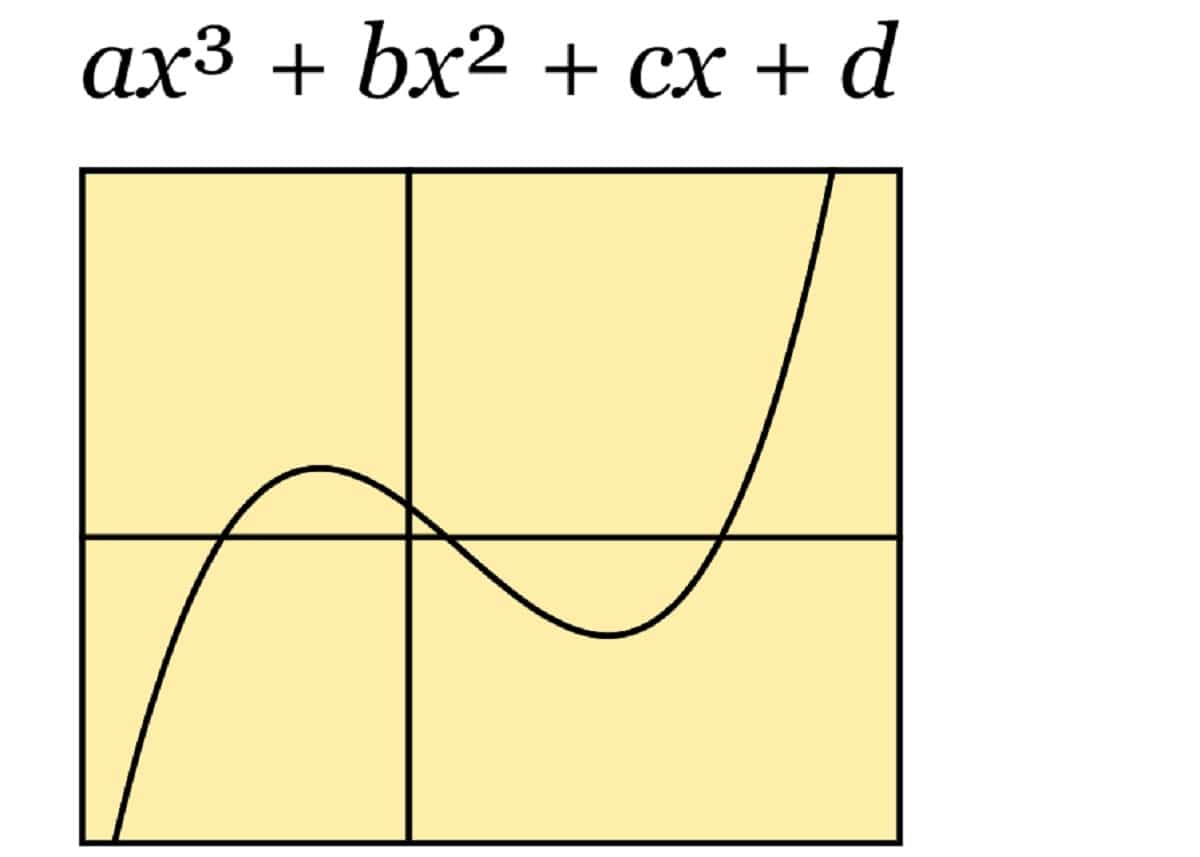
ઘન કાર્ય
અમે ત્રીજા ડિગ્રીના કાર્યો વિશે વાત કરી રહ્યા છીએ, જ્યાં સૌથી વધુ ઘાતક એક્સ વધારીને ત્રણ થાય છે. યાદ રાખો કે એ નોનઝેરો છે. તેમાં એક અથવા વધુ મૂળ પણ હોઈ શકે છે.
f (x) = કુહાડી 3 + બીએક્સ 2 + સીએક્સ + ડી
ઘાતાંકીય કાર્ય
તેના આધાર પર તેની પાસે સતત a હોય છે અને વેરીએબલ x ઘાતાદા તરીકે દેખાશે. ઘાતાંકીય કાર્યનું વ્યુત્પન્ન કાર્યના મૂલ્યના પ્રમાણમાં હશે. તેથી, આ પ્રમાણમાં સતત થવું એ આધાર બીનો કુદરતી લોગરીધમ હશે.
f (x) = અબ ×
લોગરીધમિક ફંક્શન
ઝડપી વિહંગાવલોકન મેળવવા માટે, તે કહેવું આવશ્યક છે કે તે ઘાતાંકીય વ્યક્તિનું theલટું છે. તેથી જ્યારે આપણે લોગરીધમિક વિધેયો વિશે વાત કરીએ, ત્યારે આપણે એ ઉલ્લેખ કરવો પડશે કે a એ કહ્યું ફંક્શનનો આધાર હશે, સકારાત્મક અને 1 થી અલગ.
f (x) = લ .ગax
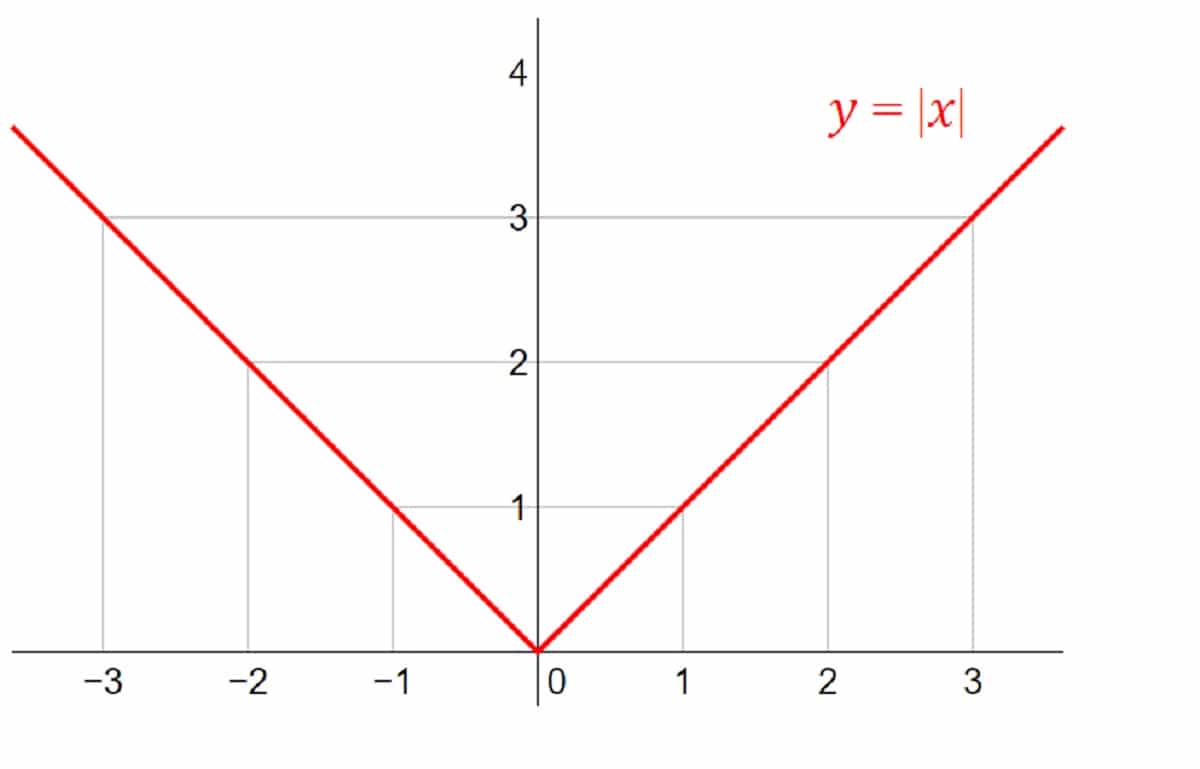
સંપૂર્ણ મૂલ્ય કાર્ય
જેમ તમે ખરેખર જાણો છો, ગણિતમાં કોઈ સંખ્યાનું સંપૂર્ણ મૂલ્ય એ તેનું સંખ્યાત્મક મૂલ્ય છે. આ કિસ્સામાં, તે હકારાત્મક છે કે નકારાત્મક છે તે ધ્યાનમાં લેવામાં આવતું નથી. કાર્યોમાં, તે તીવ્રતા અથવા અંતરથી જોડાયેલું છે. તે 0 કરતા વધારે અથવા બરાબર હશે પરંતુ ક્યારેય નકારાત્મક રહેશે નહીં.
f (x) = | x |
આ સાથે અમે દસ પ્રકારના ગાણિતિક કાર્યો સાથે વર્ગીકરણને અંતિમ સ્વરૂપ આપીએ છીએ, જે માહિતી આપણે હંમેશા હાથમાં રાખવી આવશ્યક છે કારણ કે તે સમજવું જરૂરી છે કે, આપણી સામેના કાર્યના પ્રકારને આધારે, ગ્રાફિકલ રજૂઆત નોંધપાત્ર રીતે બદલાશે , જેથી આ બધી વિગતો જાણીને, અમે ઘણું કામ કરી શકીશું કારણ કે એક પરિણામમાં અમારી પાસે પરિણામ શું છે તે જાણવા માટે બધી જરૂરી માહિતી હશે અને આપણે ગણતરી કરવાનું રહેશે નહીં.
ધ્યાનમાં રાખો કે આપણે ઘણું હાંસલ કરવા જઈ રહ્યા છીએ જો આપણે પહેલાથી જાણતા હોઈએ કે આપણે કયા પ્રકારનું પ્રતિનિધિત્વ શોધીશું, કારણ કે આ આપણને બે રીતે મદદ કરશે; સૌ પ્રથમ, અમે અવલોકન કરીશું કે બધું બરાબર પ્રગતિ કરી રહ્યું છે, એટલે કે, આપણે સ્પષ્ટ હોવું જોઈએ કે પ્રક્રિયા દરમિયાન આપણે જોશું કે આપણે સાચા ટ્રેક પર છીએ, અને બીજી બાજુ, એકવાર આપણે ગ્રાફિક રજૂઆત કરીશું , અમને પ્રાપ્ત પરિણામ યોગ્ય છે કે કેમ તે વિશે સ્પષ્ટ વિચાર હશે, કારણ કે આ ઘટનામાં કે ગ્રાફિકલ પ્રતિનિધિત્વ આપણે જે કાર્ય કરી રહ્યા છીએ તેના પ્રકારથી અલગ હતું, દેખીતી રીતે તેનો અર્થ એ થશે કે આપણે કેટલીક ગણતરીમાં મૂંઝવણ કરી લીધી છે, જેનો અર્થ છે કે આપણે તેને સુધારવા માટે ભૂલ ન મળે ત્યાં સુધી ફરી પાછા જવું પડશે અને ગ્રાફિકલ રજૂઆત સાચી છે કે નહીં તે તપાસો.
આ તમારે કાર્યોના પ્રકારો વિશે જાણવાની જરૂર છે, પરંતુ યાદ રાખો કે તમે હંમેશાં તમારા જ્ knowledgeાનને વિસ્તૃત કરો અને તે કરતાં તમે જે કવાયત કરો છો તે સમજવું, તે જ સમયે તમે શું કરી રહ્યા છો તે સમજવું, કારણ કે તે આનંદ કરવાનો એકમાત્ર રસ્તો છે ગણિત અને તે એક વિષય બનવાથી અટકાવે છે જેના માટે આપણે સારી બાજુ મેળવી શકીએ નહીં.
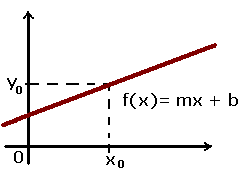
આપેલા જ્ knowledgeાન માટે આભાર. મારું કાર્ય હાથ ધરવા માટે તે મારા માટે ઉપયોગી હતું, પરંતુ જો પુસ્તક વિષયક સંદર્ભને ધ્યાનમાં રાખીને અને લખાણચોરી ન કરવા માટે મેં જે તારીખે કામ કર્યું હતું તેની સંપૂર્ણ તારીખ અને સંપૂર્ણ નામ રાખ્યું હોત તો સારું રહેશે.