वास्तविक संख्याओं का वर्गीकरण क्या है?

L वास्तविक संख्याये है तर्कसंगत और अपरिमेय संख्याओं का सेट मौजूदा से, जिनमें से विभिन्न प्रकारों को खोजना भी संभव है। ये XV और XVII सदियों के बीच पाई गई आवश्यकता के कारण पैदा हुए थे, जब गणना का तार्किक और सटीक तरीके से वर्णन करना संभव नहीं था, क्योंकि अविश्वसनीय शब्दों या अभिव्यक्तियों का उपयोग, जैसे "छोटा" या "सीमा"।

यद्यपि मिस्रियों ने पहले ही अंशों का उपयोग किया था, यह यूनानियों के गणित तक नहीं था जिसमें "संख्या" का अधिक दार्शनिक तरीके से अध्ययन किया गया था, जहां पाइथागोरस के अनुयायियों ने निष्कर्ष निकाला कि उनके चारों ओर सब कुछ संख्याएं हैं; और इसलिए, ये विभिन्न क्षेत्रों में लागू किए गए थे।

उनके प्रकार के अनुसार वास्तविक संख्याओं का वर्गीकरण

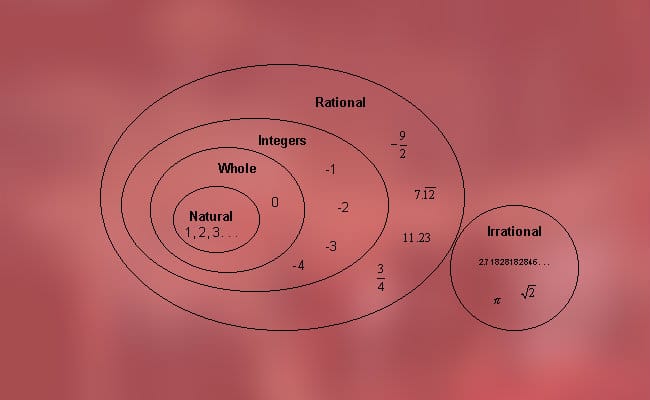
इन संख्याओं को दो प्रकारों में वर्गीकृत किया जा सकता है, जिनका हमने पहले उल्लेख किया था, वह है, परिमेय संख्या (धनात्मक, ऋणात्मक और शून्य) और अपरिमेय (बीजगणितीय और पारलौकिक)। अधिक सटीक रूप से, निम्नलिखित वर्गीकरण को खोजना संभव है:

1. परिमेय संख्या

ऐसी संख्याएँ जिनमें संपूर्ण संख्याओं के विभाजन के रूप में प्रतिनिधित्व करने की क्षमता होती है, या जो समान होती है, एक सामान्य और वर्तमान अंश जिसमें अंश और भाजक न तो शून्य होते हैं और न ही इससे कम को इस तरह कहा जाता है।

बदले में इन्हें भी कई प्रकारों में विभाजित किया जाता है: पूर्णांक (प्राकृतिक, शून्य और नकारात्मक पूर्णांक) और आंशिक (उचित और अनुचित अंश)।

ए) इंटेगर

पूर्णांक प्राकृतिक संख्याओं, ऋणात्मक पूर्णांकों और शून्य का समुच्चय होते हैं, जिन्हें "Z" अक्षर द्वारा दर्शाया जाता है। पूर्णांक भी आमतौर पर एक संख्या रेखा पर दर्शाए जाते हैं, जहां सकारात्मक या प्राकृतिक सही पर होते हैं, मध्य में शून्य और बाईं ओर नकारात्मक वाले होते हैं।

• माना जाता है "प्राकृतिक संख्याएं“उन लोगों के लिए जिनका उपयोग वस्तुओं को गिनने या कुछ अधिक सामान्य और सरल गणना कार्यों को करने के लिए किया जाता है।
• El शून्य यह एक अशक्त मूल्य है, अर्थात, जब यह साथ नहीं होता है तो किसी महत्वपूर्ण आंकड़े का अभाव होता है। हालांकि, एक संख्या में इसकी स्थिति अर्थ को पूरी तरह से बदल सकती है, जब से यह इसके दाईं ओर है जिसमें यह मूल्य को दस से गुणा करेगा; जबकि दूसरी तरफ कोई संशोधन नहीं है।
• L नकारात्मक पूर्णांक वे सकारात्मक या प्राकृतिक के विपरीत उपयोग किए जाते हैं, अर्थात्, गिनती के बजाय उनका उपयोग घटाना, बकाया करना, खर्च करना या नीचे होना है। उनका उल्लेख करने के लिए, संख्या से पहले "माइनस" शब्द को इंगित करना आवश्यक है, उदाहरण के लिए "माइनस चार"।

ख) आंशिक

वास्तविक संख्याओं के भीतर भी तर्कसंगत प्रकारों में इस प्रकार का पता लगाना संभव है, जिसकी उत्पत्ति उद्देश्य के साथ हुई थी प्राकृतिक संख्याओं के विभाजन से संबंधित समस्याओं को हल करना। एक भिन्नात्मक संख्या बस एक अभिव्यक्ति है जो एक मात्रा के विभाजन को दूसरे द्वारा इंगित करती है।

अंशों को एक अंश और हर होने की विशेषता होती है, जो एक दूसरे से एक विकर्ण या क्षैतिज पट्टी से अलग होते हैं। हालांकि, इस तथ्य के बावजूद कि पूर्णांकों में हम "सरल अंश" भी पा सकते हैं, इस खंड में हम जो भिन्न अंश पाते हैं वे उचित और अनुचित हैं।

• उचित उन लोगों से मिलकर बनता है जहां अंश भाजक से कम होता है।
• अनुचित इसके विपरीत होगा, अर्थात हर, हर से अधिक होता है।

2. अपरिमेय संख्या

तर्कहीनता वे संख्याएँ होती हैं जिनमें अंश में लिखे जाने की क्षमता नहीं होती है, क्योंकि उनके दशमलव अपने आप को लगातार दोहराते रहते हैं। उदाहरण के लिए, एक अंश लिखना असंभव है जिसमें शामिल है नंबर Pi, e, सोने और जड़ों का अनुपात वर्ग, घन, दूसरों के बीच में।

पाइथागोरस के एक छात्र को एक अंश के रूप में लिखने की आवश्यकता के लिए तर्कहीन संख्याएं उत्पन्न हुईं; यह महसूस करते हुए कि यह संभव नहीं था और यह एक संख्या थी जिसे आज हम "तर्कहीन" शब्द के तहत जानते हैं। हालाँकि, पाइथागोरस उनकी खोज से असहमत थे, हालांकि इसके लिए उन्हें अपने स्कूल के रूप में जिम्मेदार ठहराया जाता है।

इसके अलावा, इन्हें दो प्रकारों में वर्गीकृत किया जा सकता है, बीजीय और पारलौकिक।

• L बीजगणितीय वे हैं जो एक बीजीय समीकरण को हल करने की अनुमति देते हैं।
• L उत्कृष्ट वे वे हैं जो जड़ों की एक परिमित संख्या (बीजगणितीय लोगों के विपरीत) द्वारा प्रतिनिधित्व नहीं किए जा सकते हैं और जो अपने दशमलव में एक पैटर्न का पालन नहीं करते हैं। उनमें से हम पाई नंबर को पाते हैं।

अब तक हम वास्तविक संख्याओं के वर्गीकरण के साथ आते हैं, जो हमें आशा है कि पढ़ना और समझना आसान है; चूंकि बहुत से लोग गणित के प्रेमी नहीं हैं और हमने एक विस्तृत और सरल विवरण प्रदान करने की पूरी कोशिश की है।