実数の分類は何ですか？

たくさん実数です 有理数と無理数のセット 既存のものよりも、さまざまなタイプを見つけることも可能です。これらは、「小さい」や「限界」などの信頼できない用語や表現の使用が一般的で、計算を論理的かつ正確に説明することができなかったXV世紀とXVII世紀の間に見られた必要性のために生まれました。

エジプト人はすでに分数を使用していましたが、ピタゴラスの信者が彼らの周りのすべてが数であると結論付けた、より哲学的な方法で「数」が研究されたのはギリシャ人の数学までではありませんでした。したがって、これらはさまざまな分野で適用されました。

タイプによる実数の分類

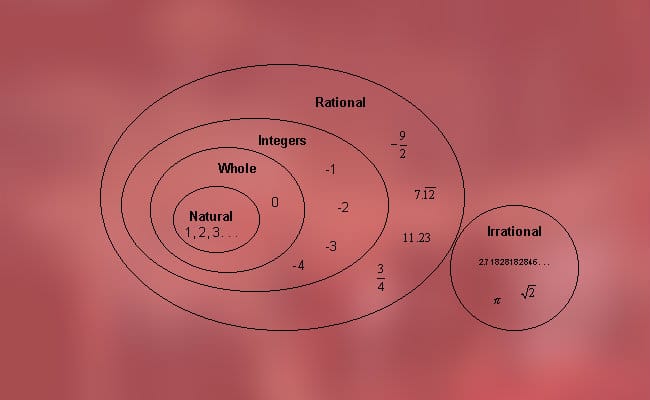
これらの数は、前述のXNUMXつのタイプ、つまり有理数（正、負、ゼロ）と無理数（代数的および超越的）に分類できます。より正確には、次の分類を見つけることができます。

整数の除算として表すことができる数、または同じもの、分子と分母がゼロでも分母でもない一般的で現在の分数は、このように呼ばれます。

これらは、整数（自然整数、ゼロ整数、負の整数）と分数（適切な分数と不適切な分数）のいくつかのタイプにも分けられます。

整数は、文字「Z」で表される自然数、負の整数、およびゼロのセットです。整数は通常、数直線で表されます。正または自然の整数は右側にあり、ゼロは中央にあり、負の整数は左側にあります。

考えられている "自然な数」アイテムを数えたり、より一般的で単純な計算操作を実行したりするのに慣れている人に。
El サワラ これはnull値です。つまり、付随していない場合は有効数字がありません。ただし、数値の右側にある場合は値にXNUMXが掛けられるため、数値内の位置によって意味が完全に変わる可能性があります。反対側では変更はありません。
たくさん 負の整数 それらは、ポジティブまたはナチュラルとは反対に使用されます。つまり、カウントする代わりに、減算、借用、支出、または以下で使用されます。それらに言及するには、数字の前に「マイナス」という用語を示す必要があります（例：「マイナスXNUMX」）。

また、実数の範囲内で、このタイプを有理数で見つけることができます。 自然数の除算に関する問題を解決します。 分数は、ある量を別の量で除算することを示す単なる式です。

分数は、分子と分母が対角線または水平のバーで互いに分離されていることを特徴としています。ただし、整数では「単純な分数」も見つけることができるという事実にもかかわらず、このセクションでは、見つけた分数のタイプは適切および不適切です。

無理数とは、小数が無限に繰り返されるため、分数で書くことができない数のことです。たとえば、を含む分数を書くことは不可能です 数円周率、e、金と根の比率 とりわけ、正方形、立方体。

ピタゴラスの生徒が分数として根を書く必要があるため、無理数が生じました。これは不可能であり、今日私たちが「不合理」という用語で知っている数であることに気づきました。しかし、ピタゴラスは彼の発見に同意しませんでしたが、それは彼の学校と同じくらい彼に起因しています。

さらに、これらは代数的と超越的のXNUMXつのタイプに分類できます。

これまでのところ、実数の分類があります。これは、読みやすく、理解しやすいものであると期待しています。多くの人は数学が好きではないので、私たちは詳細で簡単な説明を提供するために最善を尽くしました。