Wat is de classificatie van de reële getallen?

De echte getallen is set van rationele en irrationele getallen dan bestaande, waarvan het ook mogelijk is om verschillende soorten te vinden. Deze werden geboren vanwege de noodzaak die werd gevonden tussen de vijftiende en zeventiende eeuw toen de berekening niet op een logische en precieze manier kon worden beschreven, omdat het gebruikelijk was om onbetrouwbare termen of uitdrukkingen te gebruiken, zoals "klein" of "limiet".

Hoewel de Egyptenaren al breuken gebruikten, was het pas in de wiskunde van de Grieken waarin het 'getal' op een meer filosofische manier werd bestudeerd, waar de volgelingen van Pythagoras tot de conclusie kwamen dat alles om hen heen getallen zijn; en daarom werden deze toegepast in de verschillende gebieden.

Classificatie van reële getallen volgens hun type

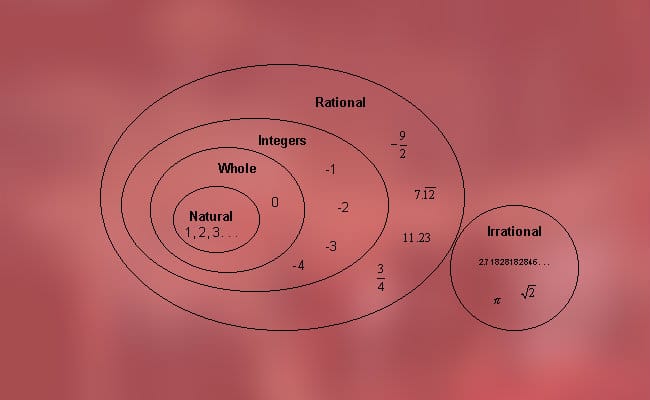
Deze getallen kunnen in twee typen worden ingedeeld, die we eerder noemden, dat wil zeggen rationale getallen (positief, negatief en nul) en irrationeel (algebraïsch en transcendentaal). Meer precies is het mogelijk om de volgende classificatie te vinden:

1. Rationale getallen

Dit is de naam die wordt gegeven aan de getallen die kunnen worden weergegeven als de deling van hele getallen, of wat hetzelfde is, een gemeenschappelijke en actuele breuk waarin de teller en de noemer niet nul of kleiner zijn.

Deze zijn op hun beurt ook onderverdeeld in verschillende typen: gehele getallen (natuurlijke, nul en negatieve gehele getallen) en fractionele (juiste en onjuiste breuken).

a) Gehele getallen

De gehele getallen zijn de verzameling natuurlijke getallen, negatieve gehele getallen en nul, die worden weergegeven door de letter "Z". De gehele getallen worden meestal ook weergegeven op een getallenlijn, waarbij de positieve of natuurlijke getallen aan de rechterkant staan, de nul in het midden en de negatieve aan de linkerkant.

• Wordt overwogen "natuurlijke cijfers”Voor degenen die gewend zijn om items te tellen of enkele van de meer gebruikelijke en eenvoudige rekenbewerkingen uit te voeren.
• El cero Het is een nulwaarde, dat wil zeggen, er ontbreekt een significant cijfer als het niet vergezeld gaat. Zijn positie in een getal kan de betekenis echter volledig veranderen, want als hij er rechts van staat, zou hij de waarde met tien vermenigvuldigen; terwijl er aan de andere kant geen wijziging is.
• De negatieve gehele getallen Ze worden gebruikt in tegenstelling tot het positieve of natuurlijke, dat wil zeggen, in plaats van te tellen, worden ze gebruikt om af te trekken, te betalen, te besteden of lager te zijn. Om ze te noemen, is het noodzakelijk om de term "min" voor het cijfer te vermelden, bijvoorbeeld "min vier".

b) fractioneel

Ook binnen de reële getallen is het mogelijk om dit type terug te vinden in de rantsoenen, die zijn ontstaan ​​met het doel van problemen oplossen met betrekking tot de deling van natuurlijke getallen. Een fractioneel getal is gewoon een uitdrukking die de deling van de ene grootheid door de andere aangeeft.

Breuken worden gekenmerkt door een teller en een noemer, die van elkaar zijn gescheiden door een diagonale of horizontale balk. Ondanks het feit dat we in de gehele getallen ook de "enkelvoudige breuk" kunnen vinden, zijn in deze sectie de soorten breuken die we vinden juist en onjuist.

• De juiste zijn die waarbij de teller kleiner is dan de noemer.
• De onjuiste zouden het tegenovergestelde zijn, dat wil zeggen, de noemer is groter dan de noemer.

2. Irrationele getallen

Irrationele getallen zijn die getallen die niet in een breuk kunnen worden geschreven, omdat hun decimalen zich oneindig blijven herhalen. Het is bijvoorbeeld onmogelijk om een ​​breuk te schrijven die de getal Pi, e, de verhouding tussen goud en wortels vierkant, kubiek, onder anderen.

Irrationele getallen zijn ontstaan ​​doordat een student van Pythagoras een wortel als breuk moest schrijven; beseffen dat dit niet mogelijk was en dat het een getal was dat we tegenwoordig kennen onder de term "irrationeel". Pythagoras was het echter niet eens met zijn ontdekking, hoewel het evenveel aan hem wordt toegeschreven als aan zijn school.

Bovendien kunnen deze worden ingedeeld in twee typen, algebraïsch en transcendentaal.

• De algebraïsch zijn die waarmee een algebraïsche vergelijking kan worden opgelost.
• De transcendent Het zijn die wortels die niet kunnen worden weergegeven door een eindig aantal wortels (in tegenstelling tot de algebraïsche wortels) en die geen patroon volgen in hun decimalen. Onder hen vinden we het nummer Pi.

Tot dusver zijn we gekomen met de classificatie van reële getallen, waarvan we hopen dat deze gemakkelijk te lezen en te begrijpen is geweest; aangezien veel mensen geen liefhebbers van wiskunde zijn en we ons best hebben gedaan om een ​​gedetailleerde en eenvoudige uitleg te geven.