Hva er klassifiseringen av de reelle tallene?

den reelle tall er sett med rasjonelle og irrasjonelle tall enn eksisterende, hvorav det også er mulig å finne forskjellige typer. Disse ble født på grunn av nødvendigheten som ble funnet mellom XV og XVII århundrer da beregningen ikke var mulig å beskrive på en logisk og presis måte, da det var vanlig å bruke upålitelige termer eller uttrykk, som "liten" eller "grense".

Selv om egypterne allerede brukte fraksjoner, var det ikke før matematikken til grekerne der "tallet" ble studert på en mer filosofisk måte, der tilhengerne av Pythagoras konkluderte med at alt rundt det er tall; og derfor ble disse brukt i de forskjellige områdene.

Klassifisering av reelle tall etter type

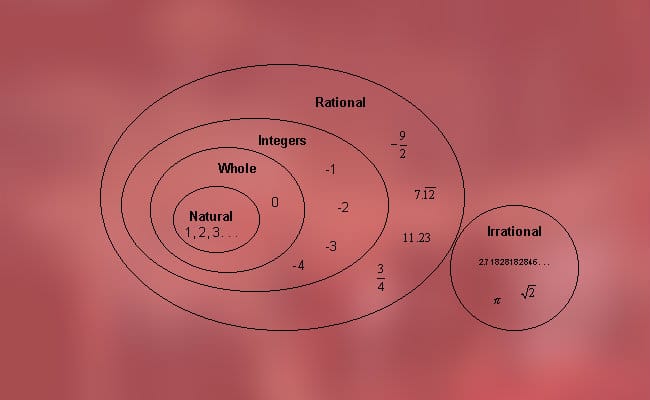
Disse tallene kan klassifiseres i to typer, som vi nevnte tidligere, det vil si rasjonelle tall (positive, negative og null) og irrasjonelle (algebraiske og transcendentale). Mer presist er det mulig å finne følgende klassifisering:

1. Rasjonelle tall

Dette er navnet gitt til tallene som har evnen til å bli representert som inndelingen av heltal, eller hva som er det samme, en vanlig og aktuell brøk der telleren og nevneren hverken er null eller mindre enn den.

Disse er i sin tur også delt inn i flere typer: heltall (naturlige, null- og negative heltall) og brøkdeler (riktige og upassende brøker).

a) Heltall

Heltallene er settet med naturlige tall, negative heltall og null, som er representert med bokstaven "Z". Heltallene er også vanligvis representert på en tallinje, der de positive eller naturlige er til høyre, null i midten og de negative til venstre.

• Regnes "naturlige tallTil de som er vant til å telle varer eller utføre noen av de mer vanlige og enkle beregningsoperasjonene.
• El Cero det er en nullverdi, det vil si at den mangler noe betydelig tall når den ikke blir ledsaget. Imidlertid kan posisjonen i et tall endre betydningen fullstendig, siden når den er til høyre for den der den ville multiplisere verdien med ti; mens det på den andre siden ikke er noen modifikasjon.
• den negative heltall De brukes i motsetning til det positive eller naturlige, det vil si i stedet for å telle, deres bruk er å trekke fra, skylde, bruke eller være under. For å nevne dem er det nødvendig å indikere begrepet "minus" før tallet, for eksempel "minus fire".

b) Brøkdel

Også innenfor de reelle tallene er det mulig å finne denne typen i rasjonellene, som stammer fra formålet med løse problemer angående inndeling av naturlige tall. Et brøknummer er ganske enkelt et uttrykk som indikerer delingen av en mengde med en annen.

Fraksjoner er preget av å ha en teller og en nevner, som er skilt fra hverandre med en diagonal eller horisontal bjelke. Til tross for det faktum at vi i heltallene også kan finne den "enkle brøkdelen", i denne delen er typer brøker vi finner, riktige og upassende.

• Deres egen består av de der telleren er mindre enn nevneren.
• De upassende ville være det motsatte, det vil si at nevneren er større enn nevneren.

2. Irrasjonelle tall

Irrasjonelle er de tallene som ikke har evnen til å bli skrevet i en brøkdel, siden desimalene deres fortsetter å gjenta seg uendelig. For eksempel er det umulig å skrive en brøkdel som inkluderer tallet Pi, e, forholdet mellom gull og røtter firkantet, kubikk, blant andre.

Irrasjonelle tall oppsto takket være behovet for en student fra Pythagoras å skrive en rot som en brøkdel; innser at dette ikke var mulig, og at det var et tall som vi i dag kjenner til under begrepet "irrasjonell". Imidlertid var Pythagoras uenig i oppdagelsen, selv om det tilskrives ham like mye som skolen hans.

Videre kan disse klassifiseres i to typer, algebraisk og transcendental.

• den algebraisk er de som tillater å løse en algebraisk ligning.
• den transcendent De er de som ikke kan representeres av et endelig antall røtter (i motsetning til de algebraiske), og som ikke følger et mønster i desimalene. Blant dem finner vi tallet Pi.

Så langt kommer vi med klassifiseringen av reelle tall, som vi håper har vært lett å lese og forstå; siden mange ikke elsker matematikk, og vi har gjort vårt beste for å gi en detaljert og enkel forklaring.