Care este clasificarea numerelor reale?

L numere reale este ansamblu de numere raționale și iraționale decât existent, dintre care este, de asemenea, posibil să se găsească diferite tipuri. Acestea s-au născut datorită necesității constatate între secolele XV și XVII când calculul nu a fost posibil să se descrie într-un mod logic și precis, fiind obișnuită utilizarea unor termeni sau expresii nesigure, precum „mic” sau „limită”.

Deși egiptenii au folosit deja fracții, abia la matematica grecilor s-a studiat „numărul” într-un mod mai filosofic, unde adepții lui Pitagora au ajuns la concluzia că tot ceea ce îi înconjoară sunt cifre; și, prin urmare, acestea au fost aplicate în diferite domenii.

Clasificarea numerelor reale în funcție de tipul lor

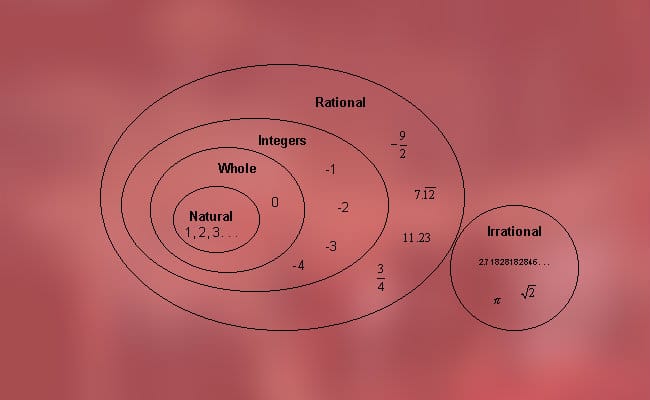
Aceste numere pot fi clasificate în două tipuri, pe care le-am menționat mai devreme, adică numere raționale (pozitive, negative și zero) și iraționale (algebrice și transcendentale). Mai precis, este posibil să se găsească următoarea clasificare:

1. Numere raționale

Acesta este numele dat numerelor care au capacitatea de a fi reprezentate ca împărțirea numerelor întregi, sau ceea ce este același, o fracție comună și curentă în care numărătorul și numitorul nu sunt nici zero, nici mai mici decât acesta.

La rândul lor, acestea sunt împărțite în mai multe tipuri: numere întregi (numere întregi naturale, zero și negative) și fracționate (fracții proprii și improprii).

a) Numere întregi

Numerele întregi sunt mulțimea numerelor naturale, întregi negative și zero, care sunt reprezentate de litera „Z”. Întregurile sunt, de asemenea, reprezentate de obicei pe o linie numerică, unde cele pozitive sau naturale sunt în dreapta, zero în mijloc și cele negative în stânga.

• Este considerat "numere naturale”Celor care sunt obișnuiți să numere elemente sau să efectueze unele dintre operațiunile de calcul mai comune și mai simple.
• El zero este o valoare nulă, adică îi lipsește orice cifră semnificativă atunci când nu este însoțită. Cu toate acestea, poziția sa într-un număr poate schimba complet sensul, deoarece atunci când este în dreapta acestuia, în care ar înmulți valoarea cu zece; în timp ce de cealaltă parte nu există nicio modificare.
• L numere întregi negative sunt folosite într-un mod contrar celor pozitive sau naturale, adică, în loc să se numere, utilizarea lor este de a scădea, datora, cheltui sau a fi mai jos. Pentru a le menționa este necesar să indicați termenul „minus” înainte de număr, de exemplu „minus patru”.

b) Fracțional

De asemenea, în cadrul numerelor reale este posibil să se găsească acest tip în raționalele, care au apărut în scopul rezolvați probleme privind împărțirea numerelor naturale. Un număr fracționat este pur și simplu o expresie care indică împărțirea unei cantități la alta.

Fracțiile sunt caracterizate prin faptul că au un numărător și un numitor, care sunt separați unul de celălalt printr-o bară diagonală sau orizontală. Cu toate acestea, în ciuda faptului că în numerele întregi putem găsi și „fracția simplă”, în această secțiune tipurile de fracții pe care le găsim sunt corecte și improprii.

• Propriile lor constau din cele în care numărătorul este mai mic decât numitorul.
• Cele necorespunzătoare ar fi opuse, adică numitorul este mai mare decât numitorul.

2. Numere iraționale

Iraționalele sunt acele numere care nu au capacitatea de a fi scrise într-o fracțiune, deoarece zecimalele lor continuă să se repete infinit. De exemplu, este imposibil să scrieți o fracție care să includă numărul Pi, e, raportul dintre aur și rădăcini pătrat, cubic, printre altele.

Numerele iraționale au apărut datorită nevoii unui student al lui Pitagora de a scrie o rădăcină ca fracție; realizând că acest lucru nu era posibil și că era un număr pe care îl cunoaștem astăzi sub termenul „irațional”. Cu toate acestea, Pitagora nu a fost de acord cu descoperirea sa, deși i se atribuie la fel de mult ca și școala sa.

Mai mult, acestea pot fi clasificate în două tipuri, algebrică și transcendentală.

• L algebric sunt cele care permit rezolvarea unei ecuații algebrice.
• L transcendent Sunt acelea care nu pot fi reprezentate de un număr finit de rădăcini (spre deosebire de cele algebrice) și care nu urmează un model în zecimalele lor. Printre acestea găsim numărul Pi.

Până acum venim cu clasificarea numerelor reale, care sperăm că a fost ușor de citit și de înțeles; deoarece mulți oameni nu sunt iubitori de matematică și am făcut tot posibilul pentru a oferi o explicație detaliată și simplă.