undefined reálne čísla je množina racionálnych a iracionálnych čísel než existujúce, z ktorých je tiež možné nájsť rôzne typy. Zrodili sa z dôvodu nevyhnutnosti medzi XV. A XVII. Storočím, keď nebolo možné logicky a presne opísať výpočet, keďže sa bežne používalo nespoľahlivých výrazov alebo výrazov, ako napríklad „malý“ alebo „limit“.
Aj keď Egypťania už používali zlomky, až v matematike Grékov sa „číslo“ študovalo filozofickejším spôsobom, kde nasledovatelia Pytagorasovho záveru dospeli k záveru, že všetko okolo neho sú čísla; a preto sa uplatňovali v rôznych oblastiach.
Klasifikácia reálnych čísel podľa ich typu
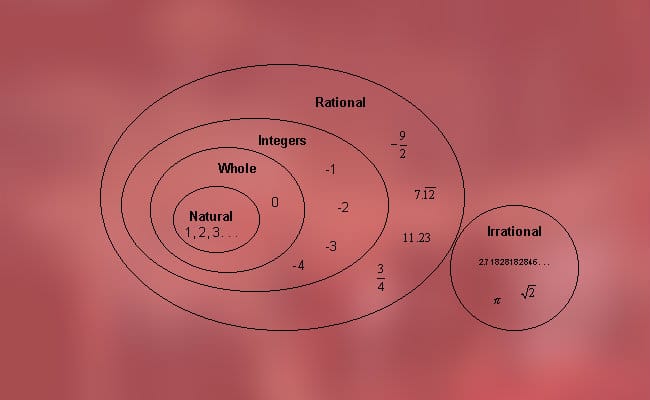
Tieto čísla je možné rozdeliť na dva typy, ktoré sme už spomenuli skôr, to znamená racionálne čísla (kladné, záporné a nulové) a iracionálne (algebraické a transcendentálne). Presnejšie je možné nájsť nasledujúcu klasifikáciu:
1. Racionálne čísla
Toto je meno, ktoré sa dáva číslam, ktoré majú schopnosť byť reprezentované ako rozdelenie celých čísel, alebo čo je rovnaké, bežný a aktuálny zlomok, v ktorom čitateľ a menovateľ nie sú ani nula, ani menšia hodnota.
Tieto sú zase rozdelené na niekoľko typov: celé čísla (prirodzené, nulové a záporné celé čísla) a zlomkové (vlastné a nesprávne zlomky).
a) Celé čísla
Celé čísla sú množinou prirodzených čísel, záporných celých čísel a nuly, ktoré sú reprezentované písmenom „Z“. Celé čísla sú tiež zvyčajne zastúpené na číselnej čiare, kde sú kladné alebo prirodzené čísla vpravo, nula v strede a záporné čísla vľavo.
- Je považovaný "prirodzené číslaTým, ktorí sa zvyknú počítať položky alebo vykonávať niektoré z bežnejších a jednoduchších výpočtových operácií.
- El nula je to nulová hodnota, to znamená, chýba jej akákoľvek významná hodnota, ak nie je uvedená. Jeho pozícia v čísle však môže úplne zmeniť význam, pretože keď je napravo od neho a vynásobí hodnotu desiatimi; zatiaľ čo na druhej strane nie je žiadna úprava.
- undefined záporné celé čísla používajú sa opačným spôsobom ako tie pozitívne alebo prirodzené, to znamená, že namiesto počítania sa používajú na odpočítanie, dlženie, utratenie alebo nižšie. Aby sme ich spomenuli, je potrebné pred číslom uviesť výraz „mínus“, napríklad „mínus štyri“.
b) Frakčné
Aj v rámci reálnych čísel je možné nájsť tento typ v racionáloch, ktoré vznikli s cieľom vyriešiť problémy týkajúce sa rozdelenia prirodzených čísel. Zlomkové číslo je jednoducho výraz, ktorý označuje rozdelenie jednej veličiny na druhú.
Frakcie sa vyznačujú tým, že majú čitateľa a menovateľa, ktoré sú navzájom oddelené diagonálnym alebo horizontálnym pruhom. Napriek tomu, že v celých číslach nájdeme aj „jednoduchú frakciu“, v tejto časti sú typy zlomkov, ktoré nájdeme, správne a nesprávne.
- Ich vlastné tvoria tie, pri ktorých je čitateľ menší ako menovateľ.
- Nesprávne by boli opakom, to znamená, že menovateľ je väčší ako menovateľ.
2. Iracionálne čísla
Iracionálne sú čísla, ktoré nie sú schopné zápisu zlomkom, pretože ich desatinné miesta sa neustále opakujú. Napríklad je nemožné napísať zlomok, ktorý obsahuje číslo Pi, e, pomer zlata a koreňov okrem iného štvorcový, kubický.
Iracionálne čísla vznikli vďaka potrebe študenta Pytagorasa napísať koreň ako zlomok; uvedomujúc si, že to nie je možné a že je to číslo, ktoré dnes poznáme pod pojmom „iracionálne“. Pytagoras však s jeho objavom nesúhlasil, aj keď sa mu pripisuje rovnako ako jeho škole.
Ďalej ich možno rozdeliť na dva typy, algebraické a transcendentálne.
- undefined algebraický sú tie, ktoré umožňujú riešenie algebraickej rovnice.
- undefined transcendentný Sú to tie, ktoré nemôžu byť reprezentované konečným počtom koreňov (na rozdiel od algebraických) a ktoré sa neriadia vzorom na svojich desatinných miestach. Medzi nimi nájdeme číslo Pi.
Zatiaľ prichádzame s klasifikáciou reálnych čísel, ktorá, ako dúfame, bola ľahko čitateľná a zrozumiteľná; pretože veľa ľudí nie je milovníkmi matematiky a my sme sa snažili poskytnúť podrobné a jednoduché vysvetlenie.
Vynikajúce vysvetlenie. Aj keď nie som popretím matematiky (som lekárnik), nepoužívam túto klasifikáciu často. Veľmi jasne a stručne.
vďaka
José
ďakujem za priazeň priateľa alebo priateľa