实数的分类是什么？

MGI 实数是 有理数和无理数集 比现有的，还可以找到各种类型。这些是由于在十五和十七世纪之间发现的需要而产生的，当时的计算无法以逻辑和精确的方式描述，通常使用不可靠的术语或表达，例如“小”或“极限”。

尽管埃及人已经使用了分数，但直到希腊人的数学以一种更为哲学的方式研究“数字”时，毕达哥拉斯的追随者们得出结论，他们周围的一切都是数字。因此，它们被应用于不同的领域。

根据实数类型对实数进行分类

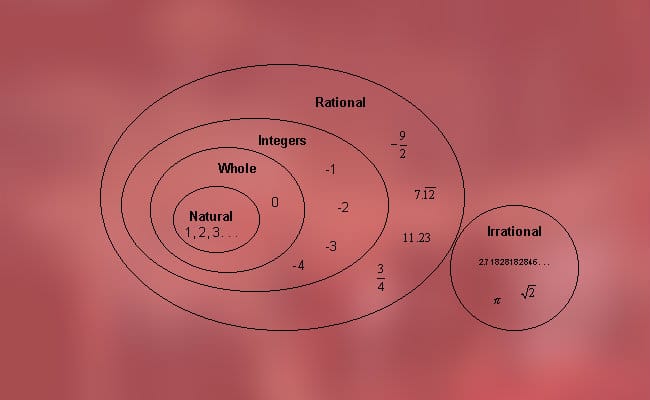
这些数字可以分为两类，我们前面已经提到过，即有理数（正数，负数和零数）和无理数（代数数和先验数）。更准确地说，可以找到以下分类：

具有这种能力的数字可以表示为整数除法，或者相同，即分子和分母既不为零也不小于其的公共和当前分数。

这些又又分为几种类型：整数（自然，零和负整数）和小数（正确和不正确的分数）。

整数是自然数，负整数和零的集合，它们由字母“ Z”表示。整数通常也用数字表示，正数或自然数在右边，零在中间，负数在左边。

被认为 ”自然数对于那些习惯于对项目进行计数或执行一些更常见和更简单的计算操作的人。
El CERO 它是一个空值，即不伴随时缺少任何有效数字。但是，它在数字中的位置可以完全改变含义，因为当它在它的右边时，它将值乘以XNUMX；另一方面，没有任何修改。
MGI 负整数 它们的使用与肯定的或自然的相反，也就是说，它们的使用不是减去，欠，花或低于，而不是计算。要提及它们，有必要在数字前标明术语“减号”，例如“减四”。

同样在实数内，有可能在有理数中找到这种类型，这是出于以下目的： 解决有关自然数除法的问题。 小数只是表示一个数量除以另一个数量的表达式。

分数的特征是具有分子和分母，它们由对角线或水平条相互分隔。但是，尽管事实上我们也可以找到“简单分数”，但在本节中，我们找到的分数类型是正确且不合适的。

无理数是指那些不能以小数形式写入的数字，因为它们的小数会继续无限重复。例如，不可能写一个包含以下内容的分数： Pi，e，金与根的比 方形，立方等。

由于毕达哥拉斯的学生需要写一个分数的根，所以出现了不合理的数字。意识到这是不可能的，并且这是今天我们在“非理性”一词下所知道的一个数字。然而，毕达哥拉斯不同意他的发现，尽管这与他的学校一样多地归功于他。

此外，它们可以分为代数和先验两种类型。

到目前为止，我们提供了实数的分类，我们希望该分类易于阅读和理解。由于许多人都不是数学爱好者，因此我们已竭尽所能提供详细而简单的解释。