Apakah klasifikasi nombor nyata?

The nombor nyata adalah set nombor rasional dan tidak rasional daripada yang ada, yang mana mungkin juga untuk mencari pelbagai jenis. Ini dilahirkan kerana keperluan yang dijumpai antara abad XV dan XVII ketika penghitungannya tidak mungkin untuk dijelaskan dengan cara yang logik dan tepat, kerana penggunaan istilah atau ungkapan yang tidak boleh dipercayai seperti biasa "kecil" atau "had".

Walaupun orang Mesir telah menggunakan pecahan, tidak sampai matematik orang Yunani di mana "nombor" dipelajari dengan cara yang lebih falsafah, di mana para pengikut Pythagoras menyimpulkan bahawa segala sesuatu di sekitar mereka adalah nombor; dan oleh itu, ini digunakan di kawasan yang berlainan.

Pengelasan nombor nyata mengikut jenisnya

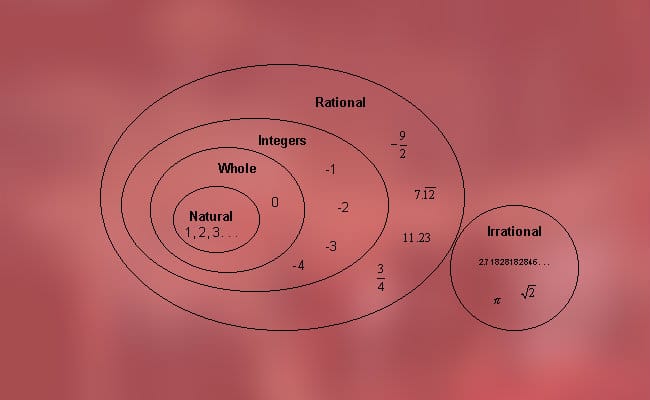
Angka-angka ini dapat diklasifikasikan menjadi dua jenis, yang telah kita sebutkan sebelumnya, iaitu nombor rasional (positif, negatif dan sifar) dan tidak rasional (algebra dan transendental). Lebih tepat lagi, adalah mungkin untuk mencari klasifikasi berikut:

1. Nombor rasional

Ini adalah nama yang diberikan kepada nombor yang memiliki kemampuan untuk diwakili sebagai pembahagian nombor bulat, atau yang sama, pecahan biasa dan semasa di mana pengangka dan penyebutnya tidak sama atau kurang dari itu.

Ini seterusnya dibahagikan kepada beberapa jenis: bilangan bulat (bilangan bulat semula jadi, sifar dan negatif) dan pecahan (pecahan wajar dan tidak wajar).

a) Bilangan bulat

Bilangan bulat adalah kumpulan nombor semula jadi, bilangan bulat negatif dan sifar, yang diwakili oleh huruf "Z". Bilangan bulat juga biasanya ditunjukkan pada garis nombor, di mana yang positif atau semula jadi berada di sebelah kanan, sifar di tengah dan yang negatif di sebelah kiri.

• Dianggap "nombor semula jadi"Kepada mereka yang terbiasa menghitung item atau melakukan operasi pengiraan yang lebih biasa dan sederhana.
• El cero Ini adalah nilai nol, iaitu, ia tidak memiliki angka yang signifikan ketika tidak disertai. Namun, posisinya dalam jumlah dapat mengubah makna sepenuhnya, kerana ketika berada di sebelah kanannya di mana ia akan menggandakan nilainya dengan sepuluh; sementara di sisi lain tidak ada pengubahsuaian.
• The bilangan bulat negatif mereka digunakan bertentangan dengan positif atau semula jadi, dan bukannya menghitung, penggunaannya adalah untuk mengurangkan, berhutang, berbelanja atau berada di bawah. Untuk menyebutnya, perlu menunjukkan istilah "tolak" sebelum angka tersebut, misalnya "tolak empat".

b) Pecahan

Juga dalam bilangan nyata adalah mungkin untuk menemukan jenis ini dalam rasional, yang berasal dengan tujuan menyelesaikan masalah mengenai pembahagian nombor semula jadi. Nombor pecahan hanyalah ungkapan yang menunjukkan pembahagian satu kuantiti dengan kuantiti yang lain.

Pecahan dicirikan dengan mempunyai pengangka dan penyebut, yang dipisahkan antara satu sama lain oleh bar pepenjuru atau mendatar. Walau bagaimanapun, walaupun dalam bilangan bulat kita juga dapat menemukan "pecahan sederhana", di bahagian ini jenis pecahan yang kita dapati tepat dan tidak tepat.

• Yang betul terdiri daripada angka yang pengangkanya kurang daripada penyebutnya.
• Yang tidak betul akan menjadi sebaliknya, iaitu, penyebutnya lebih besar daripada penyebutnya.

2. Nombor tidak rasional

Irasional adalah nombor yang tidak mempunyai kemampuan untuk ditulis dalam pecahan, kerana perpuluhan mereka terus mengulang diri mereka tanpa batas. Sebagai contoh, mustahil untuk menulis pecahan yang merangkumi nombor Pi, e, nisbah emas dan akar segi empat sama, padu, antara lain.

Nombor tidak rasional muncul berkat keperluan seorang pelajar Pythagoras untuk menulis akar sebagai pecahan; menyedari bahawa ini tidak mungkin dan bahawa itu adalah jumlah yang kita ketahui hari ini dengan istilah "tidak rasional". Walau bagaimanapun, Pythagoras tidak bersetuju dengan penemuannya, walaupun ia dikaitkan dengan sekolahnya.

Selanjutnya, ini dapat dikelaskan kepada dua jenis, algebra dan transendental.

• The algebra adalah yang membolehkan menyelesaikan persamaan algebra.
• The transenden Mereka adalah yang tidak dapat diwakili oleh jumlah akar yang terbatas (tidak seperti yang bersifat algebra) dan yang tidak mengikuti corak dalam perpuluhan mereka. Antaranya kita dapati nombor Pi.

Sejauh ini kami datang dengan klasifikasi nombor nyata, yang kami harap mudah dibaca dan difahami; oleh kerana ramai orang tidak menyukai matematik dan kami telah berusaha sebaik mungkin untuk memberikan penjelasan terperinci dan sederhana.