Het is een driedimensionale geometrische figuur die is samengesteld uit twee gelijke parallelle polygonen als bases en zijvlakken die parallellogrammen zijn. Ze krijgen een specifieke naam op basis van het aantal zijden dat hun basis vormt. We hebben dus bijvoorbeeld dat als de basis drie zijden heeft, het een driehoekig prisma zal zijn, vier rechthoekige zijden, vijf vijfhoekige zijden, enz.
Het onderwerp dat voorhanden is, heeft specifiek betrekking op alles wat ermee te maken heeft vijfhoekig prisma, maar het is noodzakelijk om de algemene aspecten van prisma's in het algemeen te kennen.
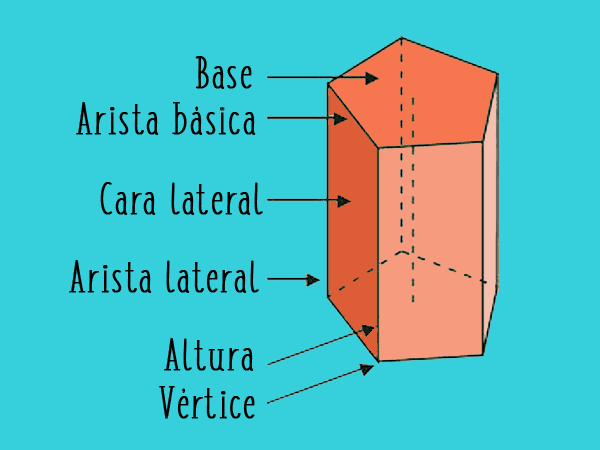
Algemene kenmerken van een prisma
Elementen waaruit een prisma bestaat:
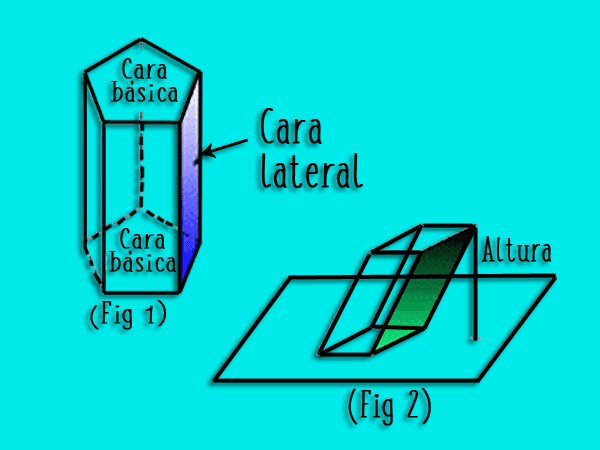
- Bases Het zijn twee parallelle en gelijke polygonen die de vloer en de bovenkant van het prisma vormen. Het aantal zijden kan variabel zijn en het zijn precies degenen die het prisma een voor- en achternaam geven.
- Zijvlakken: zijn de parallellogrammen die de onderste basis van de bovenste scheiden
- Lengte: Het is de afstand die de twee bases scheidt.
- Randen: Elk van de zijden van de polygonen die de basis vormen, worden de randen van de basis genoemd. En elk van de zijkanten van de zijvlakken wordt afzonderlijk laterale rand genoemd.
- Hoekpunt: Elk van de punten waar de randen samenkomen, wordt een hoekpunt genoemd.
Classificatie van prisma's
Een prisma wordt geclassificeerd volgens de eigenschappen van zijn bases in:
- Regelmatig:Het is er een waarvan de basis een veelhoek is waarvan alle zijden even lang zijn en ook de interne hoeken zijn van dezelfde grootte.
- Onregelmatig: Het is er een waarvan de bases worden weergegeven door polygonen met verschillende zijden en interne hoeken.
Volgens het aantal zijden dat hun bases hebben, worden ze ingedeeld in:
- Driehoekige 3 zijden
- Vierhoekig 4 zijden
- Vijfhoekige 5 zijden
- Hex 6 zijden
- Zevenhoekige 7 zijden
- Achthoekig 8 zijden
- 9-zijdige eneagon of nonagon
- Decagon 10 zijden ..., enzovoort.
Volgens hun zijvlakken worden ze ingedeeld in:
- Rechter prisma: Het is degene die zoveel zijvlakken heeft als de basis, ze zijn rechthoekig en parallel eraan.
- Schuin: Een schuin prisma heeft geen loodrechte stand op zijn zijvlakken ten opzichte van zijn basis. De zijvlakken zijn ruitvormig. Hun bijzondere kenmerk is dat hun hoogte niet samenvalt met de waarde van hun zijranden.
Volgens hun interne hoeken worden ze ingedeeld in
Concaves: Een prisma kan als concaaf worden geclassificeerd als de interne hoeken groter zijn dan 180 °. Vanwege zijn onregelmatige vorm, die het zicht geeft van een spleet naar de binnenkant van het prisma, kan deze in meer dan één punt worden gesneden als we deze met een rechte lijn kruisen.
Convex: Een prisma is convex als de interne hoeken kleiner zijn dan 180 ° en aan de andere kant hebben we dat wanneer het met een lijn wordt gekruist, het alleen op twee unieke punten snijdt.
Vijfhoekig prisma
Nu zijn we klaar om meer te leren over het vijfhoekige prisma. Zodra de kenmerken die elk prisma gemeen hebben, zijn geïdentificeerd, zullen we ons specifiek verdiepen in het vijfhoekige prisma. Een vijfhoekig prisma is een prisma waarvan de bases gelijk zijn en evenwijdige vijfhoeken en vijf parallellogrammen die de zijvlakken vormen.
Kenmerken
Het vijfhoekige prisma heeft de volgende kenmerken:
- Bases. Het heeft twee parallelle en gelijke vijfhoeken.
- Caras. Het heeft vijf zijvlakken plus de twee bases, in totaal zijn er zeven vlakken,
- Hoogte. Het is de afstand tussen de twee bases.
- Vertex. Het zijn de punten van het prisma waar drie van de vlakken samenvallen, in totaal zijn er 10 hoekpunten.
- Randen. Het zijn de ontmoetingspunten van twee van de vlakken van het prisma, in totaal heeft het 15 randen.
Volgens de stelling van Euler is er een verband tussen het aantal vlakken (C), de randen (A) en de hoekpunten van elk prisma waarvan de interne hoeken kleiner zijn dan 180 ° (convex).
Door de formule A = C + V-2 toe te passen, kan het aantal randen van een vijfhoekig prisma worden gevonden: A = 7 + 10-2 = 15
hoe Bereken de oppervlakte van een regelmatig vijfhoekig prisma
Het heeft een basis van regelmatige vijfhoeken en rechthoekige zijden gelijk, dus de berekening van het gebied wordt gegeven door:
Oppervlakte = 5. L. (ap. + H), waarbij L de maat is van een van de zijden van de vijfhoek, ap. (apothema) is de kortste afstand van het midden naar beide kanten en h is de hoogte van het prisma.
Hoe vind je de waarde van ap (apothema) van een vijfhoekig prisma?
Het is een variabele die we niet zo duidelijk kennen als de anderen. Welnu, hier is de wiskundige formule om het te vinden.
Als u het aantal zijden (N) en hun maat (L) kent, berekent u eerst de centrale hoek die wordt gevormd tussen het middelpunt van de veelhoek en twee opeenvolgende hoekpunten, als volgt:
? = 360 ° / N.
voorbeeld: centrale hoek van een vijfhoek? = 360 ° / 5 is gelijk aan 72 °.
Het volgende is de apothema
De maat van een van de zijden (L) delen door tweemaal de tangens van de helft van de centrale hoek (?)
ap = L / 2 x tang (? / 2)
Voorbeeld: met een vijfhoekig prisma waarvan de zijkanten een afmeting hebben van 20 cm en 30 centimeter hoog, laten we de oppervlakte bepalen. We weten al dat de waarde van de centrale hoek van een regelmatige vijfhoek 72 ° is. Laten we zijn apothema zoeken:
Ap = 20/2 x Tang (72/2)
Ap = 20/2 x Tang (36)
Ap = 20/2 x (0.73)
Ap = 20 / 1.46
Ap = 13,69 cm.
Nu ja, we hebben alle gegevens om uw gebied te bepalen:
Oppervlakte = 5 x L x (ap + h)
5x20 (13,69 + 30)
100 (43,69)
Oppervlakte = 4369 cm.
Oppervlakte van een onregelmatig vijfhoekig prisma
Rekening houdend met het feit dat een onregelmatig vijfhoekig prisma twee onregelmatige vijfhoeken als basis heeft, is het noodzakelijk om de oppervlakte van de onregelmatige vijfhoek (Ab), de omtrek (Pb) en de hoogte van het prisma te bepalen om later het gebied van Het prisma.
De formule voor de oppervlakte van een onregelmatig vijfhoekig rechter prisma is:
Prisma gebied = 2. Ab + Pb. h
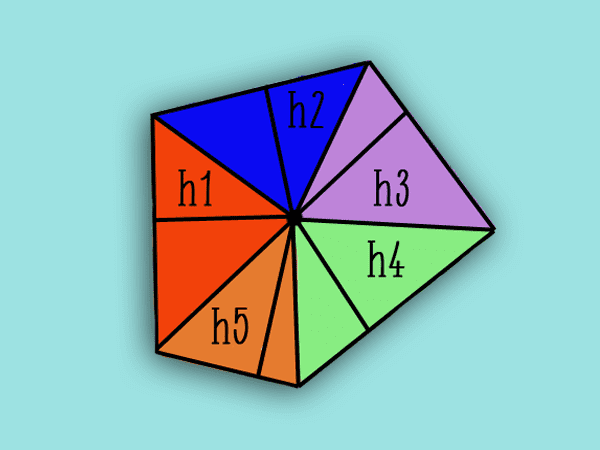
De oppervlakte van de onregelmatige basistijfhoek (Ab) wordt gevonden via de methode van triangulatie, wat betekent dat het in kleinere driehoekige figuren wordt verdeeld om hun oppervlakten te berekenen en dus gemakkelijker de totale oppervlakte van de vijfhoek wordt verkregen door ze allemaal op te tellen.
De omtrek van een onregelmatige vijfhoekige basis (Pb) Het wordt gevonden door de maat van de vijf zijden op te tellen.
Oppervlakte van een schuin vijfhoekig prisma
De formule voor het berekenen van het oppervlak voor dit type prisma verschilt van die van het rechter vijfhoekige prisma.
Het oppervlak van de bases wordt op dezelfde manier berekend als in het rechte stuk, het verschil zit in de zijkanten vanwege het feit dat ze schuin staan.
Het oppervlak van een van de zijden van een schuin vijfhoekig prisma wordt berekend op basis van de meting van een laterale rand en de omtrek van de prisma rechte sectie.
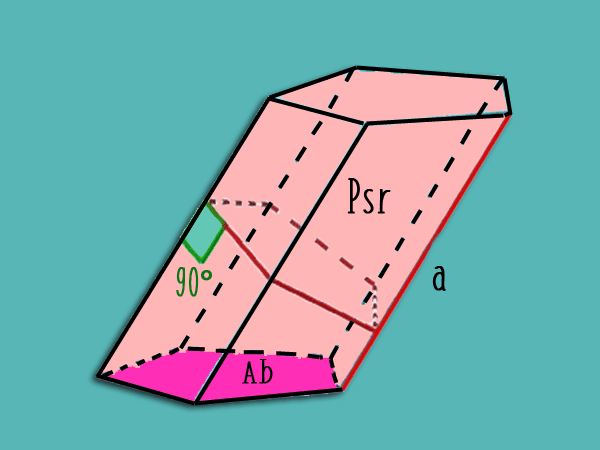
Het snijpunt van een vlak met het prisma onder een hoek van 90 ° met elk van de zijranden, is het rechte gedeelte van het prisma. Dat wil zeggen, het is de platte basis die wordt waargenomen wanneer het prisma transversaal wordt verdeeld.
Om de grafische weergave van het rechte doorsnede van een schuin prisma Iedereen, plaats het vierkant op een van de randen en teken, in een hoek van 90 °, een lijn die de aangrenzende rand bereikt, enzovoort met de andere randen. Zodra deze procedure is voltooid, kan dat oppervlak in het vliegtuig worden gevisualiseerd.
Gebied = 2. Ab + Psr. naar
waarin Ab is de oppervlakte van de basis, psr is de omtrek van het rechte gedeelte van het prisma en a een zijrand.
Om de waarde van de omtrek van het rechte gedeelte te bepalen, volstaat het om een van de randen vierkant te maken onder een hoek van 90 °, de afstand te meten van die rand tot waar deze de parallelle rand snijdt en deze vijf keer toe te voegen.
Volume van een vijfhoekig prisma
Om het volume van een vijfhoekig prisma te berekenen, zowel recht als schuin, wordt de algemene formule voor alle soorten prisma's toegepast: vermenigvuldig het oppervlak van de basis (Ab) met de hoogtemeting (h).
Volume = Ab. h
Als we Ab door zijn eigen formule vervangen, hebben we Volume = 5. L. ap / 2. h
Onthoud dat in een rechter prisma de hoogtemeting gelijk is aan de zijrandmeting terwijl in een schuin prisma de hoogte van het prisma valt niet samen met de meting van de zijrand, ongeacht het type prisma, pas op voor verwarring.
Hoe maak je een recht, regelmatig vijfhoekig prisma
? = 108 ° inwendige hoek gevormd tussen twee van de zijden van de basishoek (vaste maat voor een vijfhoekige figuur)
L = zijkant
H = hoogte
Vijfhoekige basisslag
Voordat u begint met het tekenen van het prisma, moeten de bases worden gedefinieerd. Op een makkelijke en niet zo technische manier zal ik uitleggen hoe je een regelmatige vijfhoekige figuur kunt maken.
- teken een rechte lijn die als startpunt zal dienen (fig.1)
- markeer de maat die u aan de zijkanten van uw vijfhoek wilt geven, lijn (ab) Fig.2
- Stop met behulp van een gradenboog op het punt "a "En zoek naar links naar de hoek van 108 °, trek een lijn tussen" a "en het snijpunt met de gevonden hoek en markeer daarop de maat die is gekozen voor de zijkanten van de vijfhoek. (lijn ac) afb.3
- Leun op punt b naar rechts doe dezelfde procedure als hierboven en zoek de andere kant (regel bd) fig. 4
- Leun dan op punt "c", zoek altijd naar een hoek van 108 ° en teken de (ce-lijn) fig.5
- Voeg ten slotte de ed punten samen die de ontbrekende zijde vormen. Het zou automatisch de hoek van 108 ° moeten hebben. Afb.6
Deze geometrische figuur heeft meer technische en precieze vormen voor zijn streek, maar hier leg ik het je op een eenvoudige manier uit met alleen linialen en / of vierkanten en een gradenboog.
Het succes van de constructie van uw prisma hangt af van de nauwkeurigheid van de tracering van de bases.
En de nauwkeurigheid bij de constructie van uw vijfhoekige basis zal afhangen van uw vaardigheid en kennis van de meetinstrumenten die ik voorstel.
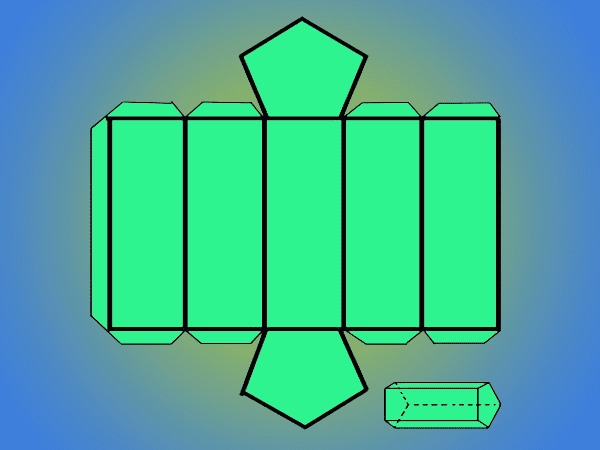
Prisma-trace
- Teken een lange rechte lijn die als basis zal dienen om de slag te beginnen.
- Markeer op die lijn de maat (L) vijf keer na elkaar.
- Teken loodrecht op elk punt de verticale lijnen die de randen voorstellen met de maat (h) hoogte.
- Verbind alle punten met een rechte lijn en je hebt een rechthoek verdeeld in vijf gelijke en evenwijdige secties, deze vertegenwoordigen elk van de zijvlakken van het prisma.
- Teken of voeg de vijfhoekige basis aan de boven- en onderkant toe op de rechthoek of het centrale vlak, of degene van uw voorkeur. Het is noodzakelijk dat je het eerst doet en op basis daarvan het prisma tekent.
- Voeg tabbladen toe aan alle zijden van de zijvlakken behalve één ervan. Deze tabbladen zullen u helpen bij het monteren van het prisma.
- Knip en breng lijm aan op de wimpers, markeer alle lijnen om het een beetje pauze te geven en maak het gemakkelijker om de randen te buigen.