Să aflăm toate tipurile de funcții matematice, ceva esențial atât pentru studenți, cât și pentru iubitorii ramurii științifice, astfel încât aceștia să obțină o bază esențială pentru a putea continua să avanseze în cunoștințele lor.
Ce sunt funcțiile matematice
O funcție este relația dintre două seturi sau mărimi în așa fel încât se stabilește o egalitate de valori între prima și a doua.
Putem reprezenta grafic o funcție, astfel încât să putem observa relația dintre ambele magnitudini, ceea ce facilitează înțelegerea acesteia și, mai presus de toate, ne deschide mintea să știm ce calculăm cu adevărat.
Amintiți-vă că matematica poate fi foarte frumoasă, dar numai dacă înțelegem procesele și obiectivele, deoarece, dacă nu avem o bază bună și ne concentrăm doar pe calcul, în cele din urmă poate ajunge să devină un subiect care se face foarte în sus . Deci, este esențial ca, pe lângă funcțiile de calcul, să petreceți ceva timp analizând semnificația lor și, pentru aceasta, cel mai bun lucru pe care îl puteți face este să le reprezentați grafic.
Toate tipurile de funcții matematice
Odată ce înțelegem conceptul unei funcții, putem continua să analizăm toate tipurile de funcții matematice care există astăzi.
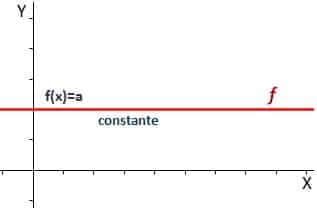
Funcția constantă
o funcție constantă Este cel în care avem un singur rezultat pentru funcția menționată, astfel încât să obținem ceva similar cu ceea ce putem vedea în următoarea imagine, adică o linie orizontală:
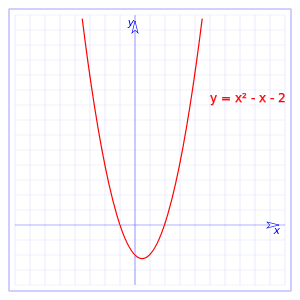
Funcția pătratică
o funcția pătratică este o funcție de tip f (x) = ax2 + bx + c, astfel încât a, b și c să fie constantele, o ființă diferită de zero în orice caz. În acest fel, ceea ce se obține este o parabolă care poate fi deschisă în sus sau în jos, în funcție de dacă a are o valoare mai mare decât zero sau dacă are o valoare mai mică de zero. Dacă este o valoare mai mare, se va deschide în sus și, dacă este mai mică decât zero, se va deschide în jos.
Trebuie menționat că funcțiile pătratice sunt funcții polinomiale.
Funcția liniară
La funtion liniar este cel care are forma f (x) = mx + b, unde m este ceea ce ne spune panta, în timp ce b este valoarea în y, astfel încât se obține o linie dreaptă, dar de data aceasta cu o anumită înclinație sau înclinare.
Este important să acordăm atenție o funcție liniară este o funcție polinomială, un tip de funcție despre care vom afla mai multe mai jos.
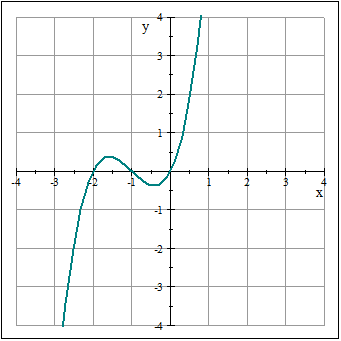
Funcția polinomială
În ceea ce privește funcția polinomială, este o funcție cu numere reale și exponenți întregi pozitivi. Trebuie remarcat faptul că domeniul tuturor funcțiilor polinomiale este mulțimea numerelor reale.
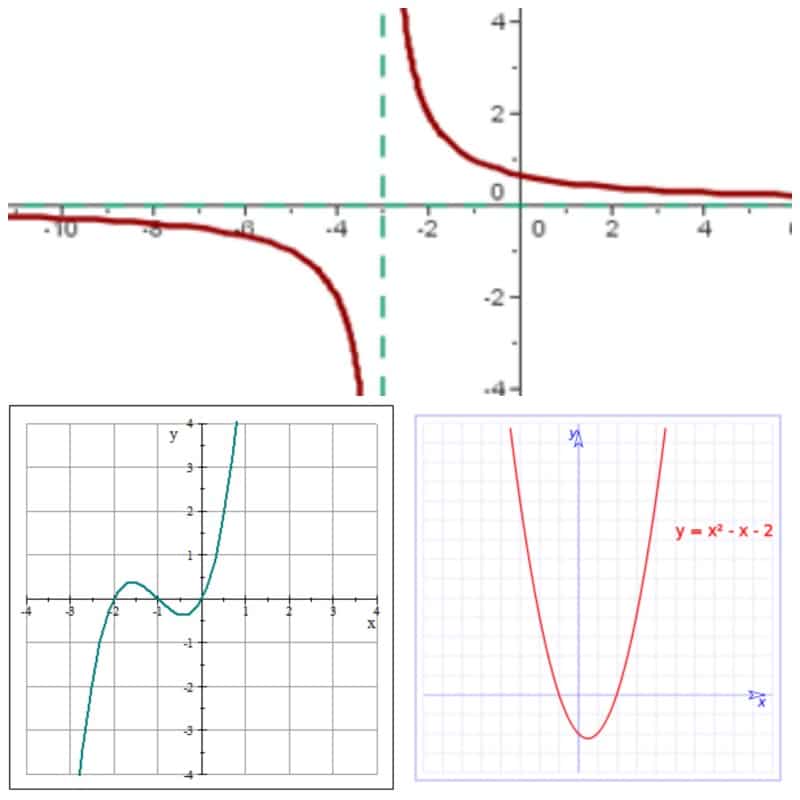
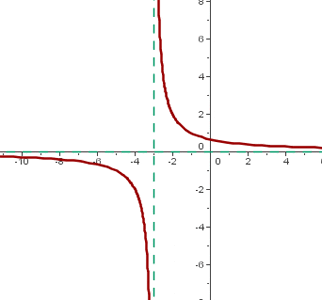
Funcția rațională
În cele din urmă avem functie rationala care este coeficientul rezultat din două funcții polinomiale, astfel încât se stabilește că q (x) = f (x) / g (x).
Un detaliu de reținut este că domeniul funcției polinomiale obține numere reale.
Funcția liniei
Când vorbim despre funcția afină, trebuie să menționăm acest lucru este o funcție polinomială. Că l-am menționat și în această listă de funcții matematice. Prin urmare, revenind la afin, este definit ca cel care nu trece prin originea coordonatelor, adică care nu atinge punctul 0,0. Sunt linii care sunt guvernate de următoarea formulă:
F (x) = mx + n
M va fi panta, adică înclinația față de axa X sau abscisa. atunci când este pozitiv, se spune că funcția crește. Deci, dacă este negativ, va fi în scădere. N va fi ordonata, punctul în care linia va tăia axa coordonatelor.
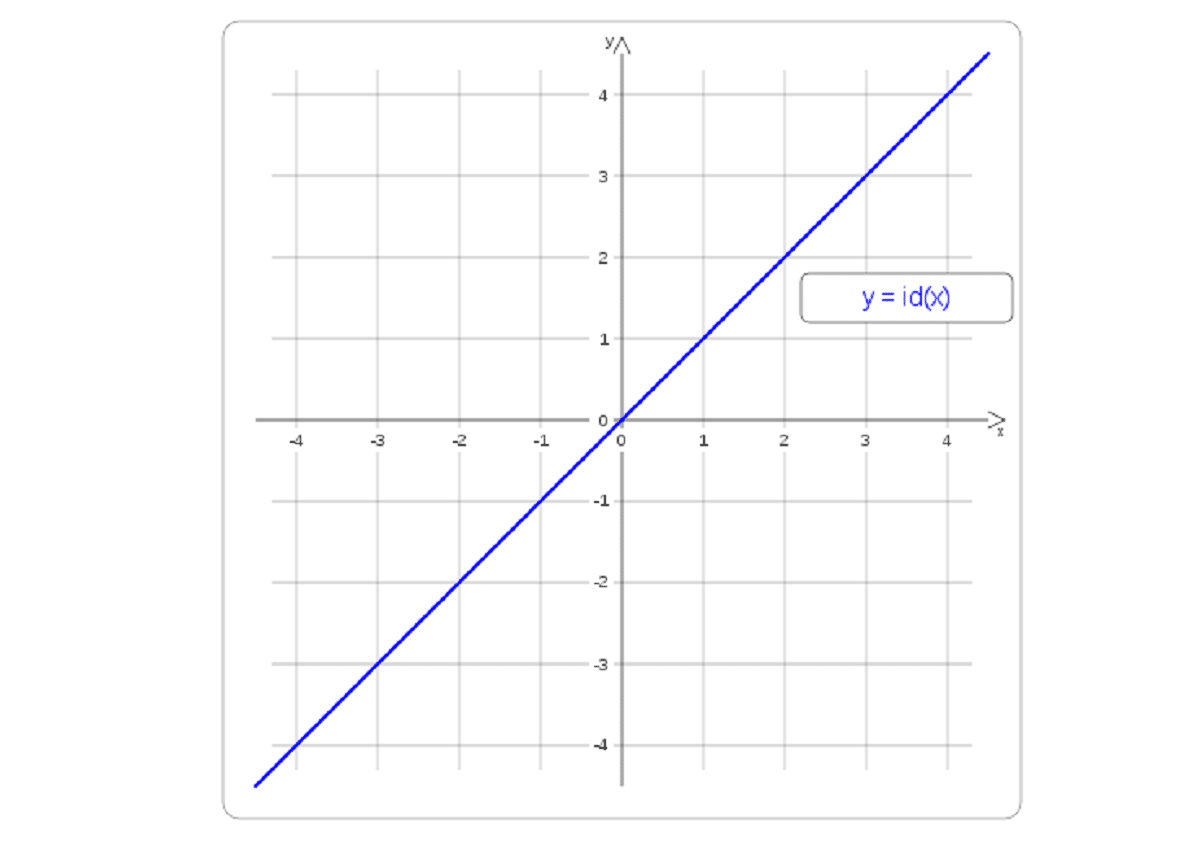
Funcția de identitate
Este funcția unui set în sine. Adică, imaginea oricărui tip de element va fi aceeași. De obicei o vedem cu id. Când vorbim despre o funcție de identitate vorbim și despre o funcție liniară, unde m este egal cu 1 și trece prin axa coordonatelor. Aceasta înseamnă că va împărți atât primul cât și al treilea cadran și ambele, în părți egale. Amintiți-vă că id-ul va fi întotdeauna elementul neutru
id r: R - R
idr(x) := x
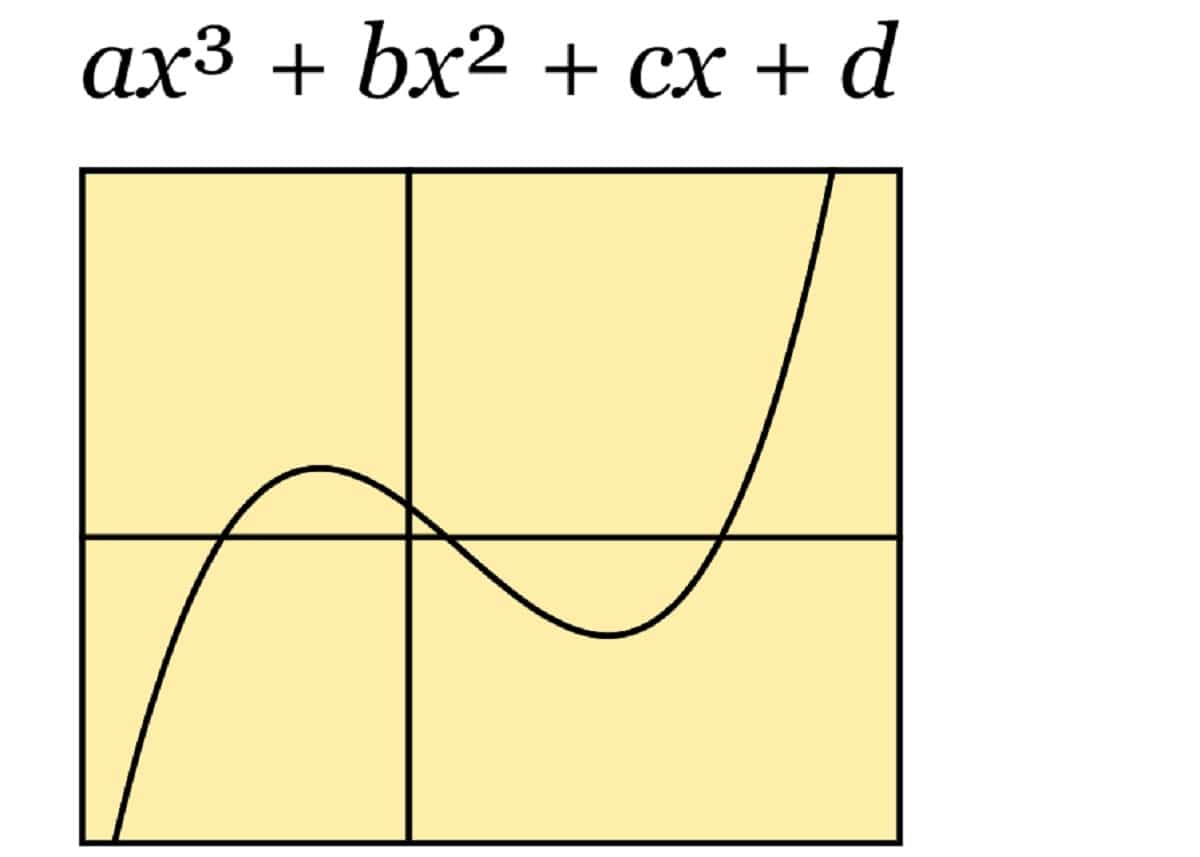
Funcția cubică
Vorbim despre funcții de gradul III, unde cel mai mare exponent este x crescut la trei. Amintiți-vă că a este diferit de zero. Poate avea, de asemenea, una sau mai multe rădăcini.
f (x) = topor 3 + bx 2 + cx + d
Functie exponentiala
La baza sa are o constantă a și variabila x va apărea ca exponent. Derivata unei funcții exponențiale va fi proporțională cu valoarea funcției. Prin urmare, constanta acestei proporționalități va fi logaritmul natural al bazei b.
f (x) = ab ×
Funcția logaritmică
Pentru a obține o imagine de ansamblu mai rapidă, trebuie spus că este inversul exponențialului. deci, atunci când vorbim despre funcții logaritmice, trebuie să menționăm că a va fi baza funcției menționate, pozitivă și diferită de 1.
f(x) = logax
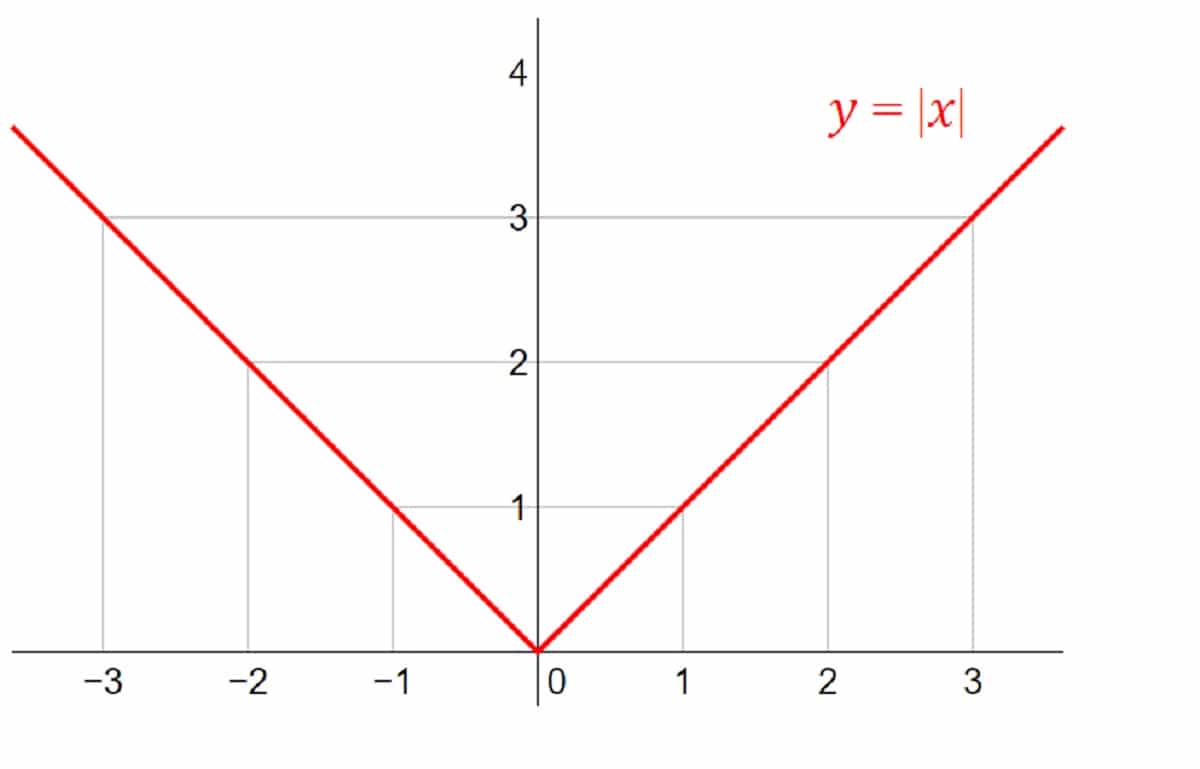
Funcția de valoare absolută
După cum știți cu siguranță, valoarea absolută a unui număr în matematică este valoarea sa numerică. În acest caz, nu se ia în considerare dacă este pozitiv sau negativ. În funcții, este legat de magnitudine sau distanțe. Acesta va fi mai mare sau egal cu 0, dar niciodată negativ.
f (x) = | x |
Cu aceasta finalizăm clasificarea cu cele zece tipuri de funcții matematice, informații pe care trebuie să le avem întotdeauna la îndemână, deoarece este esențial să înțelegem că, pe baza tipului de funcție din fața noastră, reprezentarea grafică va varia considerabil , astfel încât Cunoscând toate aceste detalii, vom putea desfășura o mulțime de muncă deoarece într-o singură privire vom avea toate informațiile necesare pentru a cunoaște care va fi rezultatul și nu va mai trebui să facem calculul.
Rețineți că vom obține multe dacă știm deja dinainte tipul de reprezentare pe care îl vom găsi, deoarece acest lucru ne va ajuta în două moduri; În primul rând, vom putea observa că totul progresează corect, adică trebuie să fim clari că în timpul procesului vom vedea că suntem pe drumul cel bun și, pe de altă parte, odată ce facem reprezentarea grafică , vom avea o idee clară despre dacă rezultatul obținut este corect, deoarece în cazul în care reprezentarea grafică a fost diferită de tipul de funcție cu care avem de-a face, în mod evident ar însemna că ne-am confundat într-un anumit calcul, ceea ce înseamnă că trebuie să ne întoarcem din nou înapoi până când se constată eroarea pentru a o corecta și a termina de verificat dacă reprezentarea grafică este corectă.
Acesta este tot ce trebuie să știți despre tipurile de funcții, dar amintiți-vă că este întotdeauna important să vă extindeți cunoștințele și, mai presus de toate, să le practicați, înțelegând în același timp ceea ce faceți, deoarece este singura modalitate de a vă bucura funcțiile.matematica și împiedică-l să devină un subiect căruia nu putem obține partea bună.
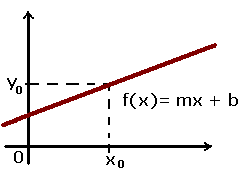
mulțumesc pentru cunoștințele oferite. Mi-a fost util să-mi desfășor activitatea, dar ar fi bine dacă aș avea data la care am făcut lucrarea și numele complet pentru a ține cont de referința bibliografică și nu pentru a plagia.