Upoznajmo sve vrste matematičkih funkcija, nešto neophodno za studente i ljubitelje naučne grane, tako da će dobiti osnovnu osnovu kako bi mogli dalje napredovati u svom znanju.
Šta su matematičke funkcije
Funkcija je odnos između dva skupa ili veličina na takav način da se uspostavlja jednakost vrijednosti između prvog i drugog.
Funkciju možemo predstaviti grafički, tako da možemo promatrati odnos između obje veličine, što olakšava njezino razumijevanje i prije svega otvara umove da znamo što zapravo računamo.
Imajte na umu da matematika može biti vrlo lijepa, ali samo ako razumijemo procese i ciljeve, jer, ako nemamo dobru osnovu i ne fokusiramo se samo na proračun, na kraju može postati predmet koji se radi vrlo uzbrdo . Stoga je neophodno da, pored izračunavanja funkcija, potrošite i neko vrijeme analizirajući njihovo značenje, a za to je najbolje što možete učiniti grafički ih prikazati.
Sve vrste matematičkih funkcija
Jednom kad shvatimo koncept funkcije, možemo nastaviti s analizom svih vrsta matematičkih funkcija koje danas postoje.
Konstantna funkcija
Una konstantna funkcija To je onaj u kojem imamo samo jedan rezultat za navedenu funkciju, tako da dobijemo nešto slično onome što možemo vidjeti na sljedećoj slici, odnosno vodoravnu crtu:
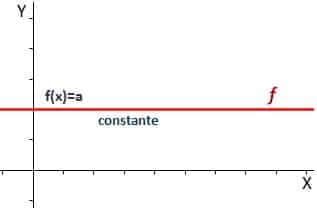
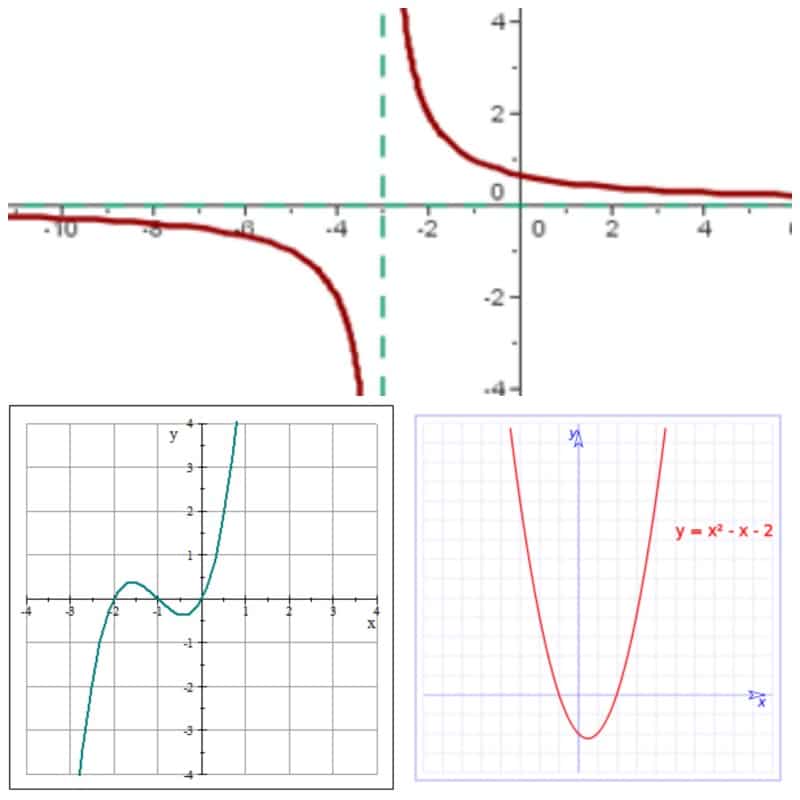
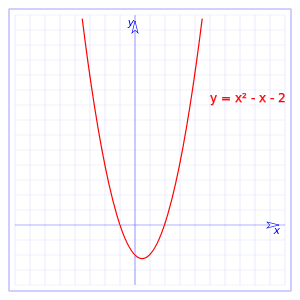
Kvadratna funkcija
Una kvadratna funkcija je funkcija tipa f (x) = ax2 + bx + c, tako da bi a, b i c bile konstante, a koje se u svakom slučaju razlikuje od nule. Na taj način se dobiva parabola koja se može otvoriti gore ili dolje, ovisno o tome ima li vrijednost veću od nule ili vrijednost manju od nule. Ako je veća vrijednost, otvorit će se prema gore, a ako je niža od nule, otvorit će se prema dolje.
Treba istaći to kvadratne funkcije su polinomske funkcije.
Linearna funkcija
La linearna funcija je onaj koji ima oblik f (x) = mx + b, gdje je m ono što nagib označava, dok je b vrijednost u y, tako da se dobiva ravna linija, ali ovaj put s određenim nagibom ili nagibom.
Važno je obratiti pažnju linearna funkcija je polinomska funkcija, tip funkcije o kojoj ćemo saznati više u nastavku.
Polinomska funkcija
Što se tiče polinomska funkcija, to je funkcija sa realnim brojevima i pozitivnim cjelobrojnim eksponentima. Treba napomenuti da je domena svih polinomskih funkcija skup realnih brojeva.
Racionalna funkcija
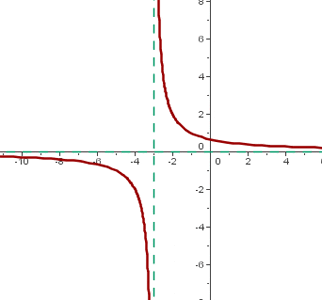
Konačno imamo racionalna funkcija što je rezultirajući količnik dviju polinomskih funkcija, tako da se utvrđuje da q (x) = f (x) / g (x).
Jedan detalj koji treba imati na umu je da područje polinomske funkcije dobiva realne brojeve.
Funkcija linije
Kada govorimo o afinoj funkciji, to moramo spomenuti to je polinomska funkcija. Da smo to spomenuli i na ovom popisu matematičkih funkcija. Stoga se, vraćajući se na afinitet, definira kao onaj koji ne prolazi kroz ishodište koordinata, odnosno koji ne dodiruje točku 0,0. To su redovi kojima upravlja sljedeća formula:
F (x) = mx + n
M će biti nagib, odnosno nagib u odnosu na X osu ili apscisu. kada je pozitivna, kaže se da se funkcija povećava. Dakle, ako je negativan, smanjivat će se. N će biti ordinata, tačka u kojoj će linija presijecati koordinatnu os.
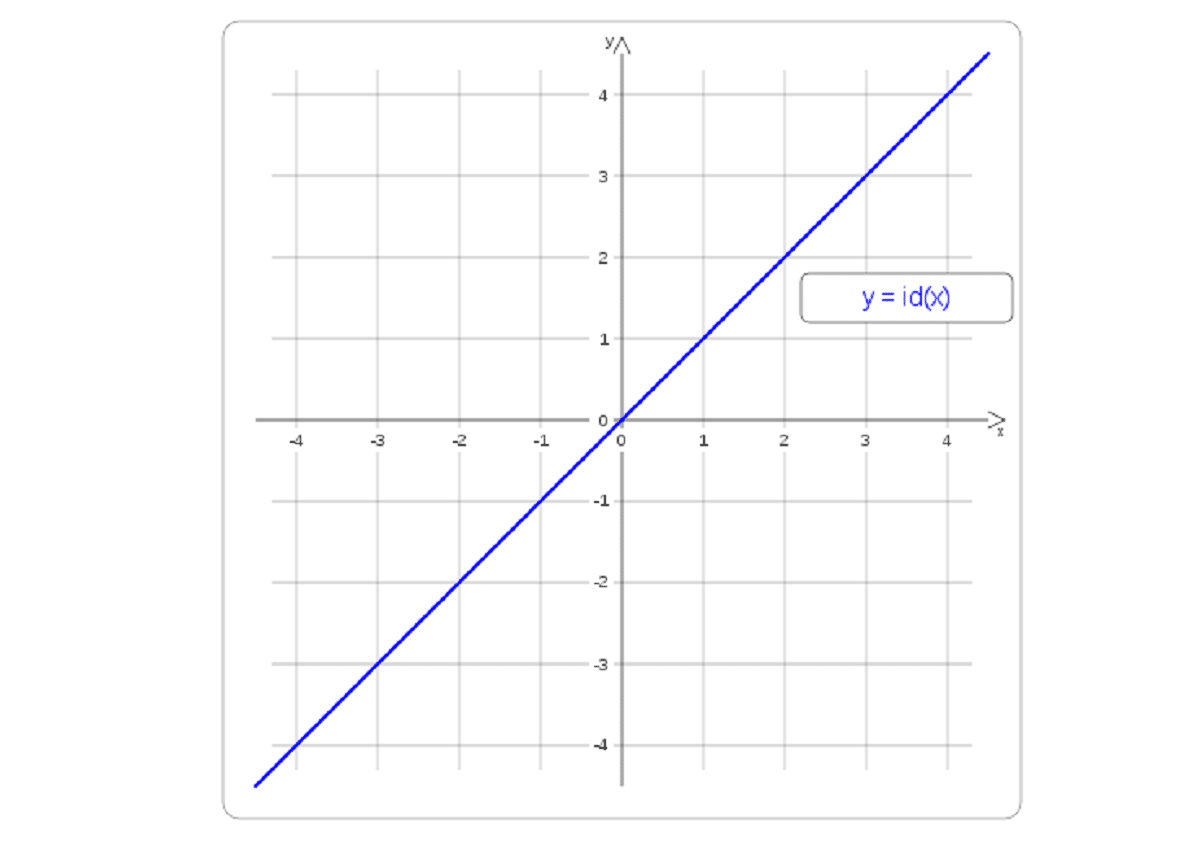
Funkcija identiteta
To je funkcija samog skupa. Odnosno, slika bilo koje vrste elementa bit će ista. Obično ga vidimo s id-om. Kada govorimo o funkciji identiteta, govorimo i o linearnoj funkciji, gdje je m jednako 1 i prolazi kroz koordinatnu os. To znači da će podijeliti i prvi i treći kvadrant i oba, podjednako. Zapamtite da će id uvijek biti neutralni element
id r: R - R
idr(x) := x
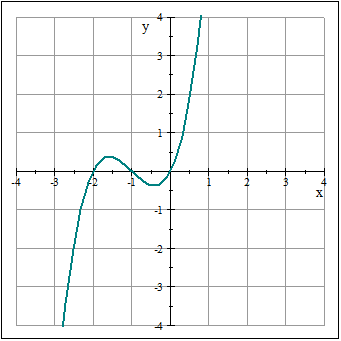
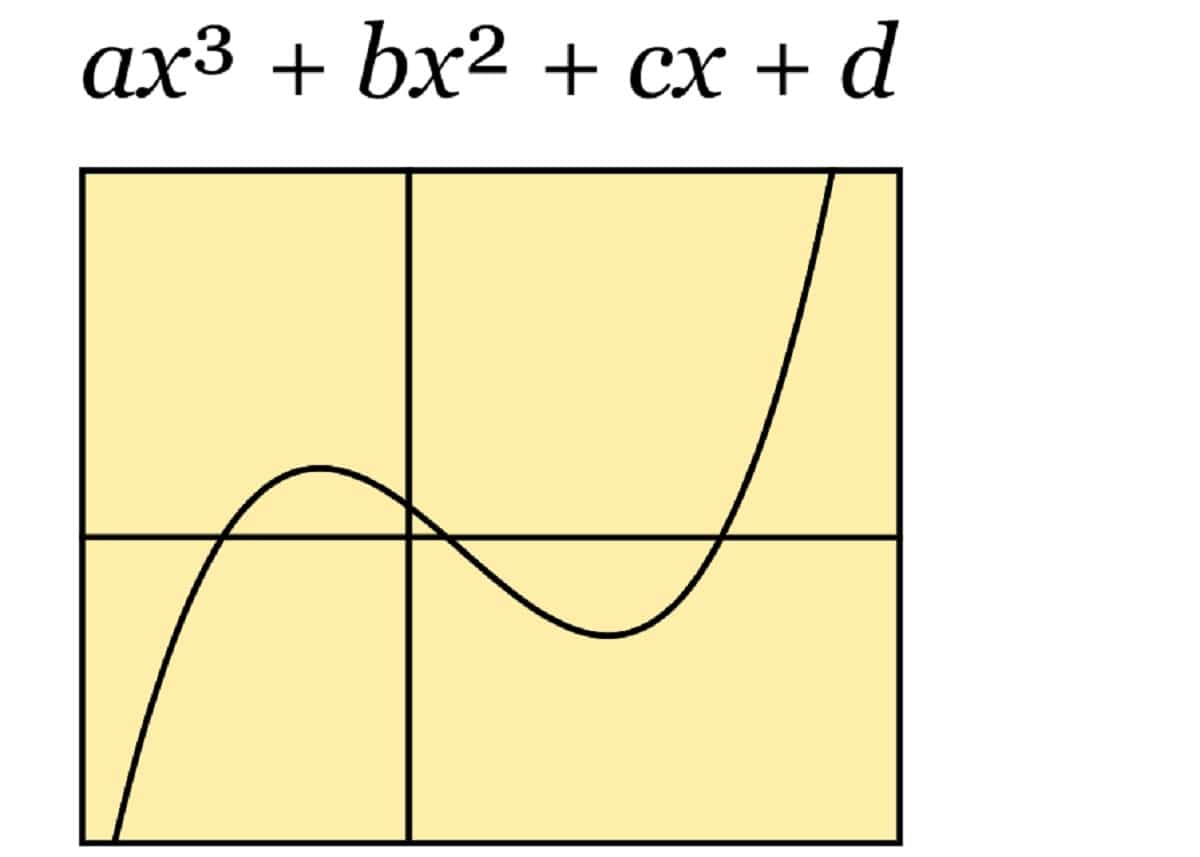
Kubična funkcija
Govorimo o funkcijama trećeg stepena, gdje je najveći eksponent x podignut na tri. Zapamtite da a nije nula. Takođe može imati jedan ili više korijena.
f (x) = os 3 + bx 2 + cx + d
Eksponencijalna funkcija
U svojoj osnovi ima konstantu a i varijabla x pojavit će se kao eksponent. Izvod eksponencijalne funkcije bit će proporcionalan vrijednosti funkcije. Dakle, konstanta ove proporcionalnosti bit će prirodni logaritam baze b.
f (x) = ab ×
Logaritamska funkcija
Da bismo dobili brži pregled, moramo reći da je to obrnuto od eksponencijala. pa kada govorimo o logaritamskim funkcijama, moramo spomenuti da će a biti osnova ove funkcije, pozitivna i različita od 1.
f(x) = logax
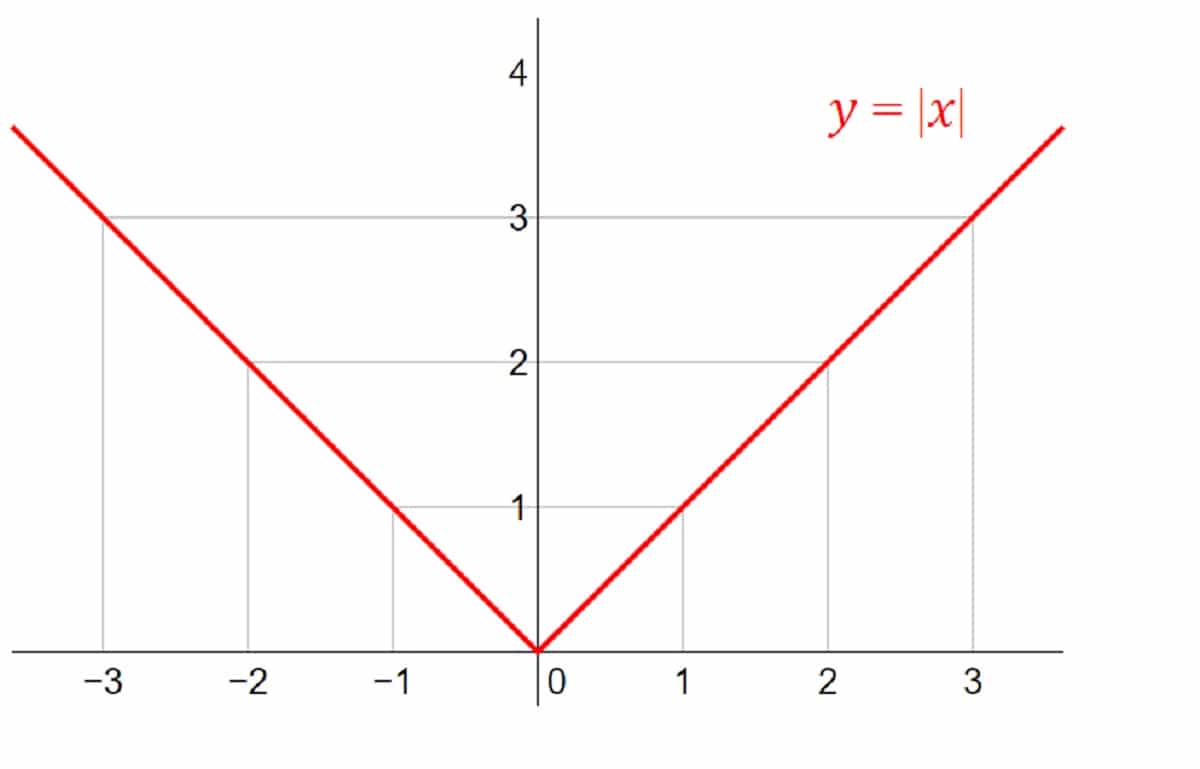
Funkcija apsolutne vrijednosti
Kao što sigurno znate, apsolutna vrijednost broja u matematici je njegova numerička vrijednost. U ovom slučaju se ne uzima u obzir da li je pozitivan ili negativan. U funkcijama je povezan s veličinom ili udaljenostima. Volja će biti veća ili jednaka 0, ali nikada negativna.
f (x) = | x |
Ovim završavamo klasifikaciju s deset vrsta matematičkih funkcija, informacijama koje moramo imati uvijek na raspolaganju, jer je neophodno da shvatimo da će se grafički prikaz znatno razlikovati na osnovu vrste funkcije koja je pred nama , tako da ćemo, znajući sve ove detalje, moći obaviti puno posla budući da ćemo jednim pogledom imati sve potrebne informacije kako bismo znali kakav će biti rezultat i više nećemo morati raditi proračun.
Imajte na umu da ćemo postići puno ako već unaprijed znamo vrstu reprezentacije koju ćemo naći, jer će nam ovo pomoći na dva načina; Prije svega, moći ćemo primijetiti da sve napreduje ispravno, to jest, moramo biti načisto da ćemo tijekom procesa vidjeti da smo na dobrom putu, a s druge strane, nakon što napravimo grafički prikaz , imat ćemo jasnu ideju o tome je li dobiveni rezultat točan, jer u slučaju da se grafički prikaz razlikuje od vrste funkcije kojom se bavimo, to bi očito značilo da smo se zbunili u nekom izračunu, što znači da se moramo vratiti unatrag dok se ne pronađe greška da bismo je ispravili i završimo provjeru ispravnosti grafičkog prikaza.
To je sve što trebate znati o vrstama funkcija, ali imajte na umu da je uvijek važno da proširite svoje znanje i prije svega vježbate, istovremeno shvaćajući što radite, jer je to jedini način da uživate funkcije matematike i spriječiti je da postane predmet koji ne možemo dobiti na dobroj strani.
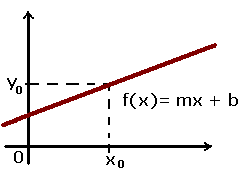
hvala na pruženom znanju. Bilo mi je korisno obavljati svoj posao, ali ako bi bilo dobro kad bih imao datum kada sam radio posao i puno ime kako bih imao na umu bibliografsku referencu i ne plagirao.