Wie ist die Klassifizierung der reellen Zahlen?

Die reale Nummern ist Satz rationaler und irrationaler Zahlen als vorhanden, von denen es auch möglich ist, verschiedene Typen zu finden. Diese wurden aufgrund der Notwendigkeit geboren, die zwischen dem XNUMX. und XNUMX. Jahrhundert bestand, als die Berechnung nicht logisch und präzise beschrieben werden konnte, da häufig unzuverlässige Begriffe oder Ausdrücke wie "klein" oder "Grenze" verwendet wurden.

Obwohl die Ägypter bereits Brüche verwendeten, wurde die "Zahl" erst in der Mathematik der Griechen philosophischer untersucht, als die Anhänger von Pythagoras zu dem Schluss kamen, dass alles um sie herum Zahlen sind; und deshalb wurden diese in den verschiedenen Bereichen angewendet.

Klassifizierung von reellen Zahlen nach ihrem Typ

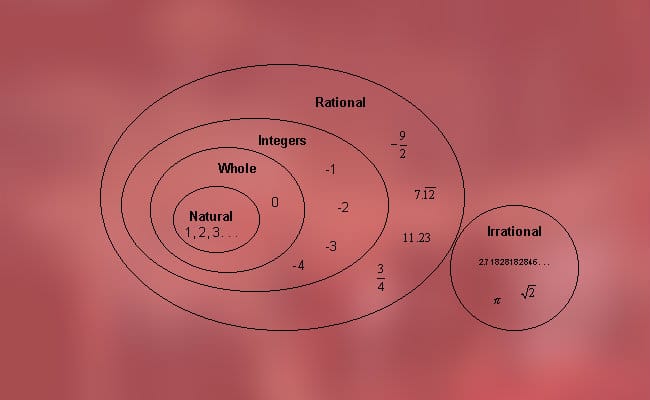
Diese Zahlen können in zwei Typen eingeteilt werden, die wir bereits erwähnt haben, nämlich die rationalen Zahlen (positiv, negativ und null) und die irrationalen (algebraisch und transzendent). Genauer gesagt ist es möglich, die folgende Klassifizierung zu finden:

1. Rationale Zahlen

Dies ist der Name, der den Zahlen gegeben wird, die als Teilung ganzer Zahlen dargestellt werden können, oder was gleich ist, ein gemeinsamer und aktueller Bruch, bei dem Zähler und Nenner weder Null noch kleiner sind.

Diese wiederum werden ebenfalls in verschiedene Typen unterteilt: Ganzzahlen (natürliche, Null- und negative Ganzzahlen) und Bruchzahlen (richtige und falsche Brüche).

a) Ganzzahlen

Die ganzen Zahlen sind die Menge von natürlichen Zahlen, negativen ganzen Zahlen und Null, die durch den Buchstaben "Z" dargestellt werden. Die ganzen Zahlen werden normalerweise auch auf einer Zahlenlinie dargestellt, wobei die positiven oder natürlichen rechts, die Null in der Mitte und die negativen links sind.

• Gilt als "natürliche Zahlen„Für diejenigen, die zum Zählen von Elementen oder zum Ausführen einiger der gängigsten und einfacheren Berechnungsvorgänge verwendet werden.
• El Cero Es ist ein Nullwert, das heißt, es fehlt eine signifikante Zahl, wenn es nicht begleitet wird. Seine Position in einer Zahl kann jedoch die Bedeutung vollständig ändern, da es rechts davon ist, in der es den Wert mit zehn multiplizieren würde; Auf der anderen Seite gibt es keine Änderungen.
• Die negative ganze Zahlen Sie werden im Gegensatz zum Positiven oder Natürlichen verwendet, das heißt, anstatt zu zählen, werden sie verwendet, um zu subtrahieren, zu schulden, auszugeben oder darunter zu sein. Um sie zu erwähnen, muss der Begriff "minus" vor der Zahl angegeben werden, beispielsweise "minus vier".

b) Bruchteil

Auch innerhalb der reellen Zahlen ist es möglich, diesen Typ in den Rationalen zu finden, die mit dem Zweck von entstanden sind Probleme bezüglich der Teilung natürlicher Zahlen lösen. Eine Bruchzahl ist einfach ein Ausdruck, der die Division einer Größe durch eine andere angibt.

Brüche zeichnen sich durch einen Zähler und einen Nenner aus, die durch einen diagonalen oder horizontalen Balken voneinander getrennt sind. Trotz der Tatsache, dass wir in den ganzen Zahlen auch den „einfachen Bruch“ finden können, sind in diesem Abschnitt die Arten von Brüchen, die wir finden, richtig und unangemessen.

• Die richtigen bestehen aus solchen, bei denen der Zähler kleiner als der Nenner ist.
• Die falschen wären das Gegenteil, das heißt, der Nenner ist größer als der Nenner.

2. Irrationale Zahlen

Irrationals sind solche Zahlen, die nicht in Bruchteilen geschrieben werden können, da sich ihre Dezimalstellen weiterhin unendlich wiederholen. Zum Beispiel ist es unmöglich, einen Bruch zu schreiben, der das enthält Zahl Pi, e, das Verhältnis von Gold und Wurzeln quadratisch, kubisch, unter anderem.

Irrationale Zahlen entstanden dank der Notwendigkeit eines Schülers von Pythagoras, eine Wurzel als Bruch zu schreiben; zu erkennen, dass dies nicht möglich war und dass es eine Zahl war, die wir heute unter dem Begriff "irrational" kennen. Pythagoras war jedoch mit seiner Entdeckung nicht einverstanden, obwohl sie ihm ebenso zugeschrieben wird wie seiner Schule.

Darüber hinaus können diese in zwei Typen eingeteilt werden, algebraisch und transzendent.

• Die algebraisch sind solche, die das Lösen einer algebraischen Gleichung ermöglichen.
• Die transzendent Sie sind diejenigen, die nicht durch eine endliche Anzahl von Wurzeln dargestellt werden können (im Gegensatz zu den algebraischen) und die in ihren Dezimalstellen keinem Muster folgen. Unter ihnen finden wir die Nummer Pi.

Bisher kommen wir mit der Klassifizierung von reellen Zahlen, von denen wir hoffen, dass sie leicht zu lesen und zu verstehen sind. da viele Menschen keine Liebhaber der Mathematik sind und wir unser Bestes getan haben, um eine detaillierte und einfache Erklärung zu liefern.