Milline on tegelike arvude klassifikatsioon?

osa reaalarvud on ratsionaalsete ja irratsionaalsete arvude kogum olemasolevatest, millest on võimalik leida ka erinevaid tüüpe. Need sündisid vajaduse tõttu, mis leiti XV ja XVII sajandi vahel, kui arvutust ei olnud võimalik loogiliselt ja täpselt kirjeldada, olles levinud ebausaldusväärsete terminite või väljendite, näiteks "väike" või "piir", kasutamine.

Ehkki egiptlased kasutasid juba murdosa, uuriti "numbrit" filosoofilisemal viisil alles kreeklaste matemaatikas, kus Pythagorase järgijad jõudsid järeldusele, et kõik selle ümber on arvud; ja seetõttu rakendati neid erinevates valdkondades.

Reaalarvude klassifitseerimine nende tüübi järgi

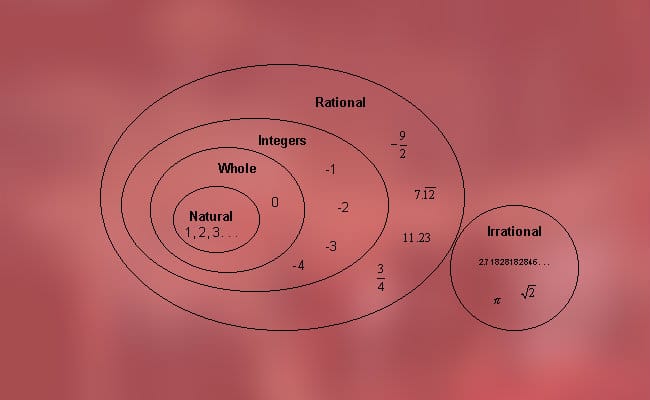
Neid numbreid saab liigitada kahte tüüpi, mida me varem mainisime, see tähendab ratsionaalsed arvud (positiivsed, negatiivsed ja nullid) ja irratsionaalsed (algebralised ja transtsendentaalsed). Täpsemalt on võimalik leida järgmine klassifikatsioon:

1. Ratsionaalarvud

See on nimi, mis antakse numbritele, mida on võimalik esindada täisarvude jaguna, või mis on sama, ühine ja praegune murd, milles lugeja ja nimetaja pole null ega väiksem kui see.

Need jagunevad omakorda mitmeks tüübiks: täisarvud (looduslikud, null- ja negatiivsed täisarvud) ja murdarvud (õiged ja sobimatud murrud).

a) täisarvud

Täisarvud on looduslike arvude, negatiivsete täisarvude ja nulli hulk, mida tähistab täht "Z". Täisarvud on tavaliselt esindatud ka numbrireal, kus positiivsed või loomulikud on paremal, null keskel ja negatiivsed vasakul.

• Peetakse "looduslikud arvudNeile, kes on harjunud kaupade loendamiseks või mõne tavalisema ja lihtsama arvutustoimingu sooritamiseks.
• El null see on nullväärtus, see tähendab, et sellel pole olulist numbrit, kui sellega ei kaasne. Kuid selle asukoht arvus võib tähendust täielikult muuta, sest kui see on sellest paremal, kus see korrutaks väärtuse kümnega; samal ajal kui teisel poolel pole muudatusi.
• osa negatiivsed täisarvud neid kasutatakse vastupidiselt positiivsetele või loomulikele, see tähendab, et loendamise asemel on nende kasutamine lahutamine, omamine, kulutamine või alla jäämine. Nende mainimiseks on vaja numbri ette märkida mõiste "miinus", näiteks "miinus neli".

b) murdosa

Ka reaalarvude sees on seda tüüpi võimalik leida ratsionaalsetest põhjustest, mis algasid selle eesmärgiga looduslike arvude jagamisega seotud probleemide lahendamine. Murdarv on lihtsalt avaldis, mis näitab ühe suuruse jagamist teisega.

Fraktsioone iseloomustab lugeja ja nimetaja olemasolu, mis on üksteisest eraldatud diagonaalse või horisontaalse riba abil. Hoolimata asjaolust, et täisarvudest võime leida ka „lihtsa murdosa“, on selles jaotises leitavad murdude tüübid õiged ja sobimatud.

• Nende omad koosnevad neist, kus lugeja on väiksem kui nimetaja.
• Sobimatud oleksid vastupidised, see tähendab, et nimetaja on suurem kui nimetaja.

2. Irratsionaalsed arvud

Irratsionaalsed on need arvud, mida pole võimalik kirjutada murdosa, kuna nende kümnendkohad jätkavad end lõpmatult. Näiteks on võimatu kirjutada murdosa, mis sisaldab arv Pi, e, kulla ja juurte suhe ruut, kuup, muu hulgas.

Irratsionaalsed arvud tekkisid tänu Pythagorase õpilase vajadusele kirjutada juur murru kujul; mõistes, et see pole võimalik ja et see on number, mida täna teame mõistega "irratsionaalne". Kuid Pythagoras ei nõustunud tema avastusega, ehkki seda omistatakse talle sama palju kui tema koolile.

Lisaks saab neid jagada kahte tüüpi, algebralistesse ja transtsendentaalsetesse.

• osa algebraline on need, mis võimaldavad lahendada algebralist võrrandit.
• osa transtsendentne Need on need, mida ei saa esindada lõpliku arvu juurtega (erinevalt algebralistest) ja mis ei järgi nende kümnendkohtade mustrit. Nende hulgast leiame numbri Pi.

Siiani oleme jõudnud reaalarvude klassifikatsiooniga, mida loodetavasti on olnud lihtne lugeda ja mõista; kuna paljud inimesed pole matemaatika austajad ja oleme teinud kõik endast oleneva, et anda üksikasjalik ja lihtne selgitus.