Apa klasifikasi bilangan real?

Los bilangan real adalah kumpulan bilangan rasional dan irasional selain yang ada, yang juga memungkinkan untuk menemukan berbagai jenis. Ini lahir karena kebutuhan yang ditemukan antara abad XV dan XVII ketika penghitungan tidak memungkinkan untuk dijelaskan secara logis dan tepat, karena penggunaan istilah atau ekspresi yang tidak dapat diandalkan, seperti "kecil" atau "batas", merupakan hal yang umum.

Meskipun orang Mesir sudah menggunakan pecahan, baru pada matematika Yunani di mana "bilangan" dipelajari dengan cara yang lebih filosofis, di mana para pengikut Pythagoras menyimpulkan bahwa segala sesuatu di sekitar mereka adalah angka; dan oleh karena itu, ini diterapkan di area yang berbeda.

Klasifikasi bilangan real menurut tipenya

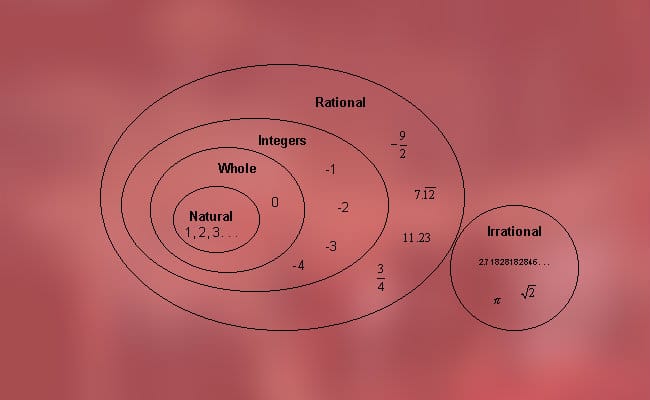
Angka-angka ini dapat diklasifikasikan menjadi dua jenis, yang telah kami sebutkan sebelumnya, yaitu bilangan rasional (positif, negatif dan nol) dan irasional (aljabar dan transendental). Lebih tepatnya, dimungkinkan untuk menemukan klasifikasi berikut:

1. Bilangan rasional

Bilangan yang memiliki kemampuan untuk direpresentasikan sebagai pembagian bilangan bulat, atau yang sama, pecahan umum dan saat ini di mana pembilang dan penyebutnya tidak nol atau kurang dari itu disebut demikian.

Ini pada gilirannya juga dibagi menjadi beberapa jenis: bilangan bulat (bilangan bulat alami, nol dan negatif) dan pecahan (pecahan tepat dan tidak tepat).

a) Bilangan bulat

Bilangan bulat adalah himpunan bilangan asli, bilangan bulat negatif dan nol, yang diwakili oleh huruf "Z". Bilangan bulat juga biasanya direpresentasikan pada garis bilangan, di mana yang positif atau alami ada di sebelah kanan, nol di tengah dan yang negatif di sebelah kiri.

• Dianggap "bilangan asliBagi mereka yang terbiasa menghitung item atau melakukan beberapa operasi penghitungan yang lebih umum dan sederhana.
• El nol Ini adalah nilai nol, yaitu tidak memiliki angka yang signifikan jika tidak disertai. Namun, posisinya dalam sebuah bilangan dapat sepenuhnya mengubah artinya, karena di sebelah kanannya ia akan mengalikan nilainya dengan sepuluh; Sedangkan di sisi lain tidak ada modifikasi.
• Los bilangan bulat negatif mereka digunakan dengan cara yang berlawanan dengan yang positif atau alami, artinya, alih-alih menghitung, penggunaannya adalah untuk mengurangi, memiliki, membelanjakan, atau berada di bawah. Untuk menyebutkannya perlu untuk menunjukkan istilah "minus" sebelum angka, misalnya "minus empat".

b) Pecahan

Juga dalam bilangan real adalah mungkin untuk menemukan jenis ini dalam rasio, yang berasal dari tujuan memecahkan masalah tentang pembagian bilangan asli. Bilangan pecahan hanyalah ekspresi yang menunjukkan pembagian satu kuantitas dengan kuantitas lainnya.

Pecahan dicirikan dengan memiliki pembilang dan penyebut, yang dipisahkan satu sama lain oleh batang diagonal atau horizontal. Namun, terlepas dari kenyataan bahwa dalam bilangan bulat kita juga dapat menemukan “pecahan sederhana”, pada bagian ini jenis pecahan yang kita temukan adalah tepat dan tidak tepat.

• Mereka sendiri terdiri dari orang-orang di mana pembilangnya lebih kecil dari penyebutnya.
• Yang tidak tepat adalah sebaliknya, yaitu, penyebutnya lebih besar dari penyebutnya.

2. Bilangan irasional

Irasional adalah angka-angka yang tidak memiliki kemampuan untuk dituliskan dalam pecahan, karena desimalnya terus berulang tanpa batas. Misalnya, tidak mungkin untuk menulis pecahan yang menyertakan nomor Pi, e, rasio emas dan akar persegi, kubik, antara lain.

Bilangan irasional muncul berkat kebutuhan siswa Pythagoras untuk menulis akar sebagai pecahan; menyadari bahwa ini tidak mungkin dan bahwa itu adalah angka yang kita kenal sekarang dengan istilah "irasional". Namun, Pythagoras tidak setuju dengan penemuannya, meskipun itu dikaitkan dengan dia sebagai sekolahnya.

Selanjutnya, ini dapat diklasifikasikan menjadi dua jenis, aljabar dan transendental.

• Los aljabar adalah orang-orang yang memungkinkan penyelesaian persamaan aljabar.
• Los transenden Mereka adalah mereka yang tidak dapat diwakili oleh jumlah akar yang terbatas (tidak seperti yang aljabar) dan yang tidak mengikuti pola dalam desimalnya. Di antara mereka kami menemukan angka Pi.

Sejauh ini kami datang dengan klasifikasi bilangan real, yang kami harap mudah dibaca dan dipahami; karena banyak orang bukan pecinta matematika dan kami telah melakukan yang terbaik untuk memberikan penjelasan yang mendetail dan sederhana.