Mari kenali semua jenis fungsi matematik, sesuatu yang penting bagi pelajar dan pencinta cabang ilmiah, supaya mereka mendapat asas penting untuk terus maju dalam pengetahuan mereka.
Apakah fungsi matematik
Fungsi adalah hubungan antara dua set atau kuantiti sedemikian rupa sehingga persamaan nilai terjalin antara yang pertama dan yang kedua.
Kita dapat menggambarkan fungsi secara grafik sehingga kita dapat melihat hubungan antara kedua-dua besarnya, yang memudahkan pemahamannya dan di atas segalanya membuka minda kita untuk mengetahui apa yang sebenarnya kita hitung.
Ingatlah bahawa matematik boleh menjadi sangat indah tetapi hanya jika kita memahami proses dan objektifnya, kerana, jika kita tidak mempunyai asas yang baik dan hanya fokus pada pengiraan, pada akhirnya ia dapat menjadi subjek yang dilakukan dengan sangat menanjak . Oleh itu, penting untuk, selain mengira fungsi, anda juga meluangkan masa untuk menganalisis maksudnya dan, untuk ini, yang terbaik yang boleh anda lakukan adalah menunjukkannya secara grafik.
Semua jenis fungsi matematik
Setelah kita memahami konsep fungsi, kita dapat terus menganalisis semua jenis fungsi matematik yang ada sekarang.
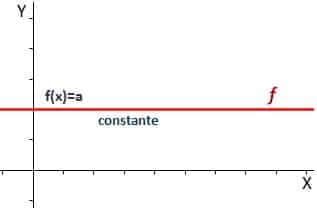
Fungsi berterusan
yang fungsi berterusan Ini adalah satu di mana kita hanya mempunyai satu hasil untuk fungsi tersebut, sehingga kita memperoleh sesuatu yang serupa dengan apa yang dapat kita lihat pada gambar berikut, iaitu garis mendatar:
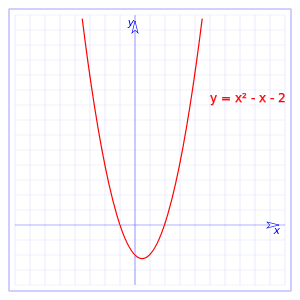
Fungsi kuadratik
yang fungsi kuadratik adalah fungsi jenis f (x) = ax2 + bx + c, jadi a, b dan c akan menjadi pemalar, yang berbeza dari sifar dalam apa jua keadaan. Dengan cara ini, apa yang diperoleh adalah parabola yang dapat dibuka ke atas atau ke bawah, bergantung pada apakah nilai memiliki nilai lebih besar dari nol, atau jika nilai tersebut kurang dari nol. Sekiranya ia adalah nilai yang lebih tinggi, ia akan terbuka ke atas, dan jika nilai itu lebih rendah dari sifar, ia akan terbuka ke bawah.
Perlu diingatkan bahawa fungsi kuadratik adalah fungsi polinomial.
Fungsi linear
La fungsi talian adalah yang mempunyai bentuk f (x) = mx + b, di mana m adalah apa yang ditunjukkan oleh cerun, sementara b adalah nilai dalam y, sehingga garis lurus diperoleh tetapi kali ini dengan kecenderungan atau kemiringan tertentu.
Penting untuk diberikan perhatian fungsi linear adalah fungsi polinomial, jenis fungsi yang akan kita ketahui lebih lanjut di bawah.
Fungsi polinomial
Sebagai fungsi polinomial, ini adalah fungsi dengan bilangan nyata dan eksponen bilangan bulat positif. Perlu diingatkan bahawa domain semua fungsi polinomial adalah kumpulan nombor nyata.
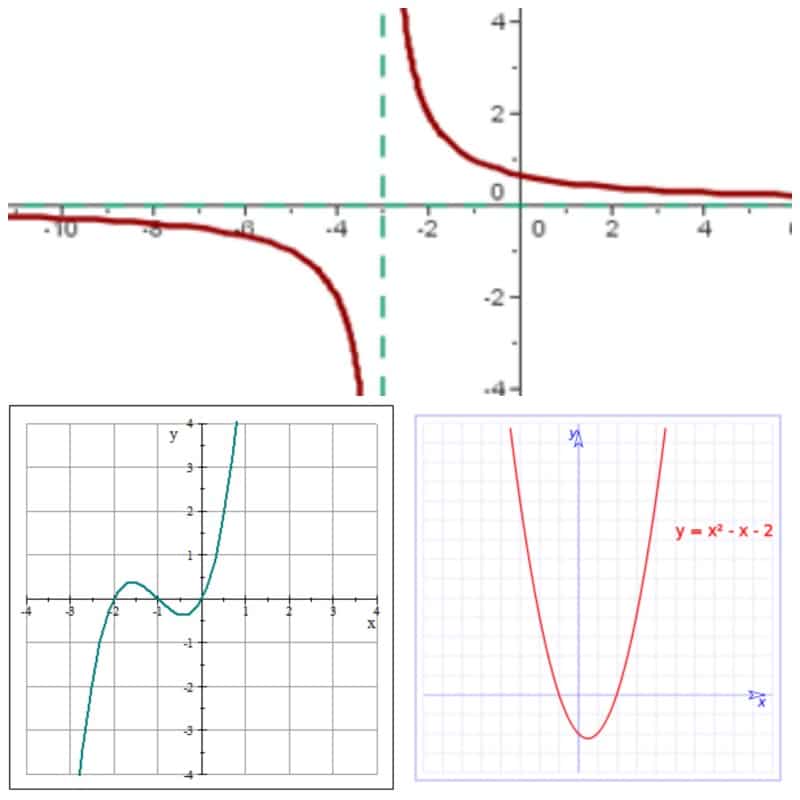
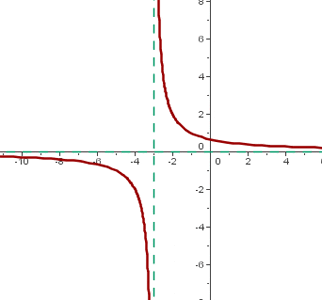
Fungsi rasional
Akhirnya kita mempunyai fungsi rasional yang merupakan hasil bagi dua fungsi polinomial, sehingga ditentukan bahawa q (x) = f (x) / g (x).
Satu perincian yang perlu diingat adalah bahawa domain fungsi polinomial memperoleh nombor nyata.
Fungsi talian
Apabila kita bercakap mengenai fungsi afin, kita mesti menyebutnya ia adalah fungsi polinomial. Kita juga telah menyebutnya dalam senarai fungsi matematik ini. Oleh itu, kembali ke garis pertalian, didefinisikan sebagai yang tidak melewati asal koordinat, iaitu, tidak menyentuh titik 0,0. Mereka adalah garis yang diatur oleh formula berikut:
F (x) = mx + n
M akan menjadi lereng, iaitu, kecenderungan berkenaan dengan sumbu X atau abses. apabila positif, fungsi tersebut dikatakan semakin meningkat. Jadi jika negatif, ia akan berkurang. N akan menjadi ordinat, titik di mana garis akan memotong paksi koordinat.
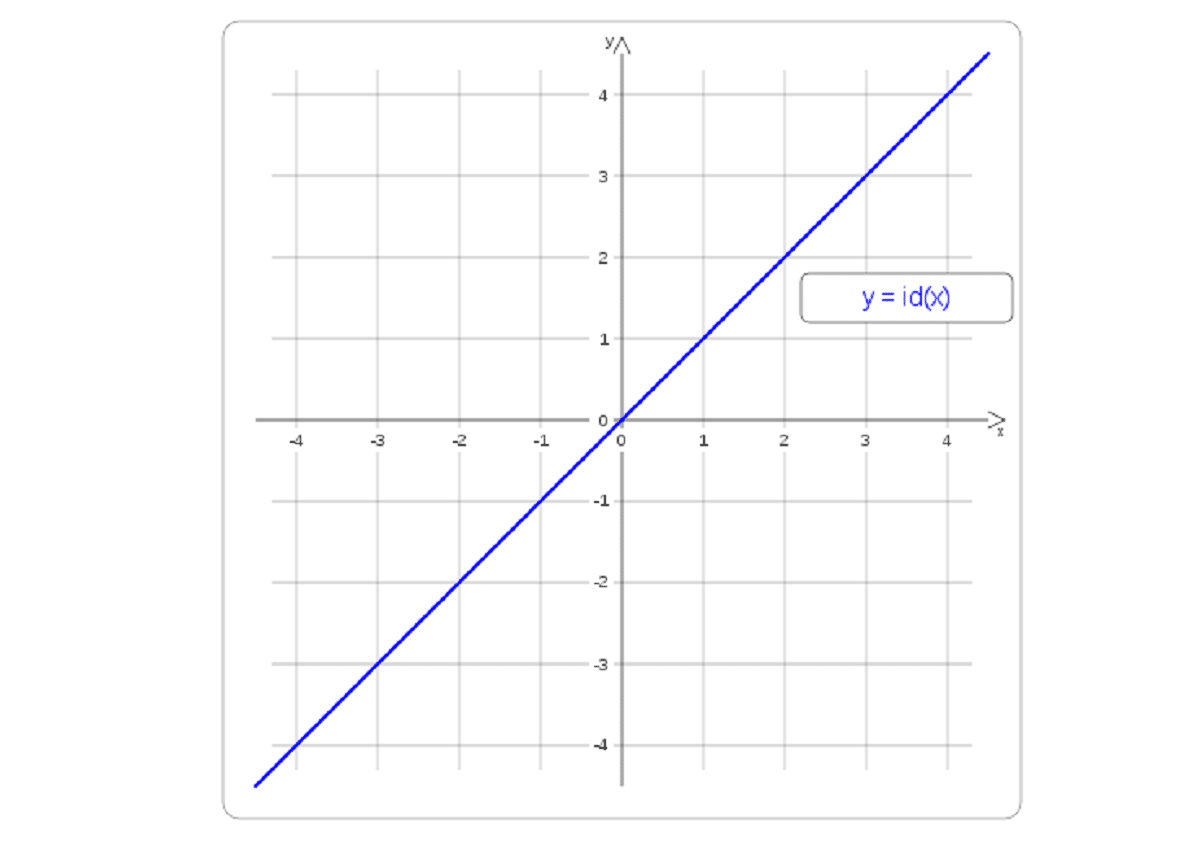
Fungsi identiti
Ini adalah fungsi satu set itu sendiri. Maksudnya, gambar unsur jenis apa pun akan sama. Kami biasanya melihatnya dengan id. Apabila kita bercakap mengenai fungsi identiti, kita juga bercakap mengenai fungsi linear, di mana m sama dengan 1 dan melewati paksi koordinat. Ini bermaksud bahawa ia akan membahagi kuadran pertama dan ketiga dan kedua-duanya, dalam bahagian yang sama. Ingat bahawa id akan selalu menjadi unsur neutral
id r: R - R
idr(x) := x
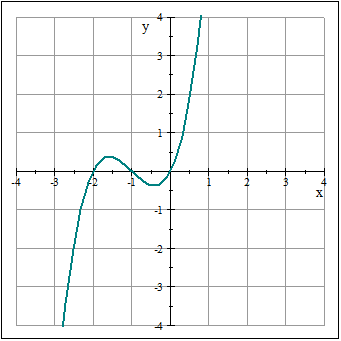
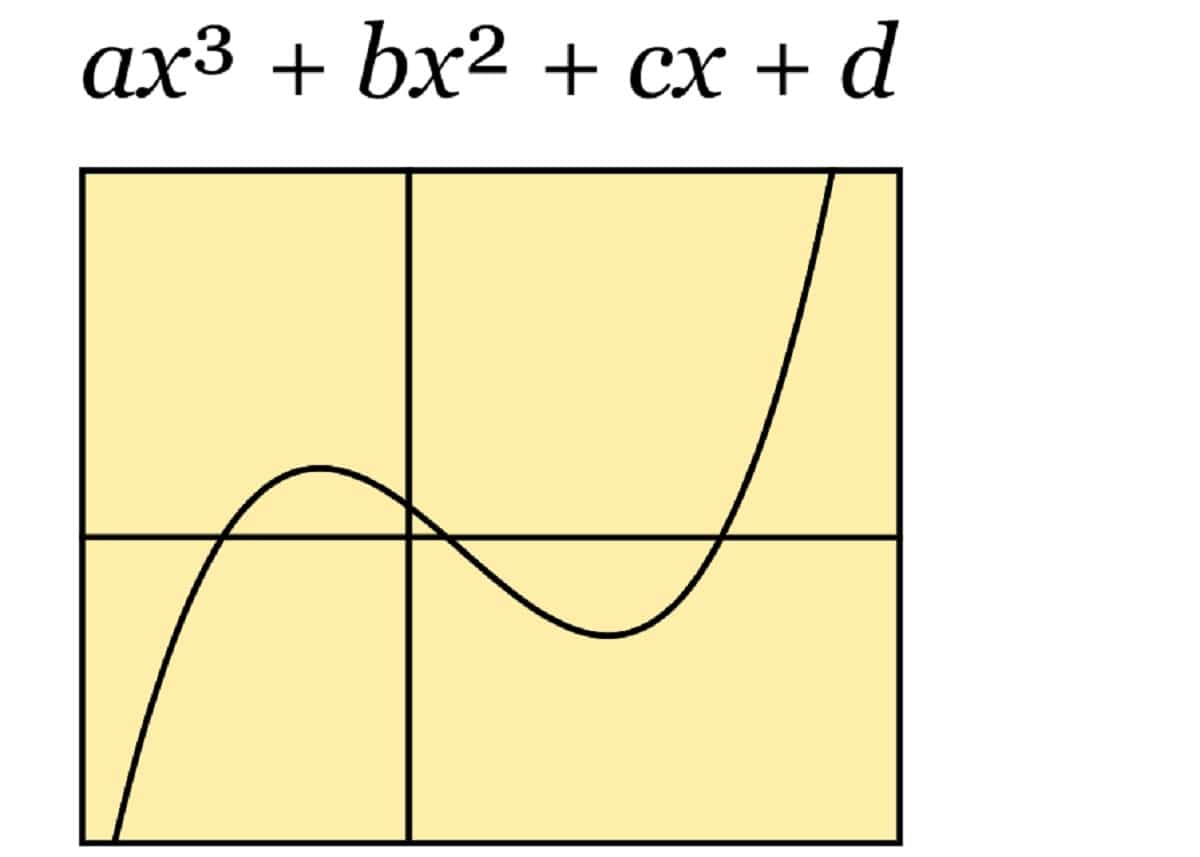
Fungsi kubik
Kita bercakap mengenai fungsi darjah ketiga, di mana eksponen terbesar adalah x dinaikkan menjadi tiga. Ingat bahawa a adalah bukan sifar. Ia juga boleh mempunyai satu atau lebih akar.
f (x) = kapak 3 + bx 2 + cx + d
Fungsi eksponen
Pada dasarnya ia mempunyai pemalar a dan pemboleh ubah x akan muncul sebagai eksponen. Derivatif fungsi eksponensial akan sebanding dengan nilai fungsi. Oleh itu, pemalar berkadar ini akan menjadi logaritma semula jadi pangkalan b.
f (x) = ab ×
Fungsi logaritma
Untuk mendapatkan gambaran keseluruhan yang lebih cepat, mesti dikatakan bahawa ia adalah kebalikan dari eksponen. jadi ketika kita membincangkan fungsi logaritmik, kita harus menyebut bahawa kehendak akan menjadi asas fungsi ini, positif dan berbeza dari 1.
f(x) = logax
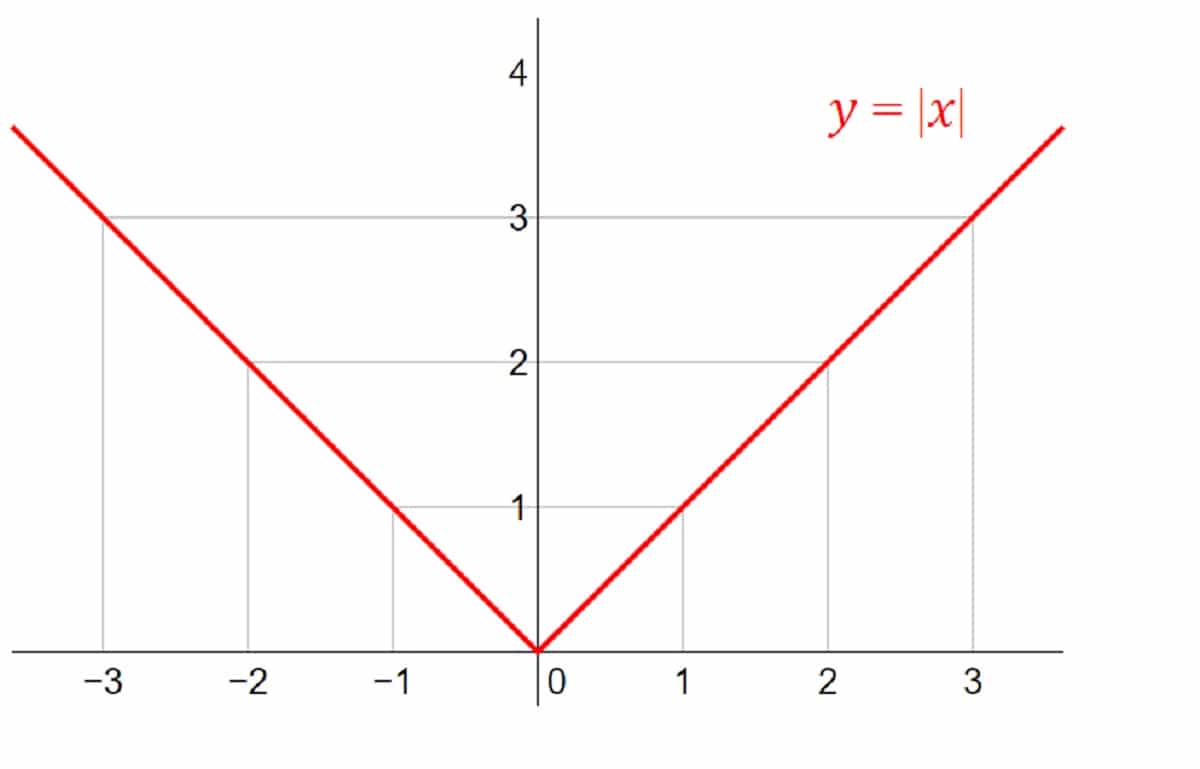
Fungsi nilai mutlak
Seperti yang anda pasti ketahui, nilai mutlak bagi nombor dalam matematik adalah nilai berangka. Dalam kes ini, tidak diambil kira sama ada positif atau negatif. Dalam fungsi, ia dihubungkan dengan magnitud atau jarak. Ia akan lebih besar daripada atau sama dengan 0 tetapi tidak pernah negatif.
f (x) = | x |
Dengan ini kita menyelesaikan klasifikasi dengan sepuluh jenis fungsi matematik, maklumat yang mesti kita selalu ada kerana penting untuk kita memahami bahawa, berdasarkan jenis fungsi di hadapan kita, representasi grafik akan sangat berbeza. , Dengan mengetahui semua butiran ini, kami akan dapat melakukan banyak pekerjaan kerana dengan sekali pandangan kami akan memiliki semua maklumat yang diperlukan untuk mengetahui hasilnya dan kami tidak perlu lagi melakukan pengiraan.
Ingatlah bahawa kita akan mencapai banyak jika kita sudah mengetahui terlebih dahulu jenis representasi yang akan kita temui, kerana ini akan membantu kita dengan dua cara; Pertama sekali, kita akan dapat melihat bahawa semuanya berjalan dengan betul, iaitu, kita mesti jelas bahawa semasa proses kita akan melihat bahawa kita berada di landasan yang benar, dan di sisi lain, setelah kita membuat perwakilan grafik , kita akan memiliki idea yang jelas tentang apakah hasil yang diperoleh itu benar, kerana jika perwakilan grafik berbeza dari jenis fungsi yang kita hadapi, itu jelas berarti kita telah bingung dalam beberapa perhitungan, yang berarti bahawa kita harus kembali lagi ke belakang sehingga mendapati kesalahan untuk membetulkannya dan selesai memeriksa bahawa perwakilan grafik betul.
Ini semua yang perlu anda ketahui mengenai jenis fungsi, tetapi ingatlah bahawa selalu penting anda memperluas pengetahuan anda dan di atas semua yang anda praktikkan, memahami pada masa yang sama apa yang anda lakukan, kerana itu adalah satu-satunya cara untuk menikmati fungsi, matematik dan menghalangnya daripada menjadi mata pelajaran yang tidak dapat kita perolehi.
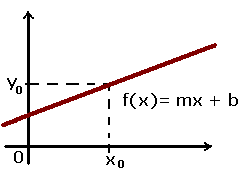
terima kasih atas pengetahuan anda yang diberikan. Ia berguna bagi saya untuk melaksanakan kerja saya tetapi akan lebih baik jika saya mempunyai tarikh saya membuat kerja dan nama penuh untuk mengingat rujukan bibliografi dan tidak melakukan penipuan.