Какова классификация реальных чисел?

вещественные числа является набор рациональных и иррациональных чисел чем существующие, из которых также можно найти различные типы. Они возникли в связи с необходимостью, обнаруженной между XV и XVII веками, когда расчет невозможно было описать логически и точно, поскольку часто использовались ненадежные термины или выражения, такие как «малый» или «предел».

Хотя египтяне уже использовали дроби, это было до тех пор, пока математика греков не изучала «число» более философски, когда последователи Пифагора пришли к выводу, что все вокруг них является числами; и поэтому они применялись в различных областях.

Классификация действительных чисел по их типу

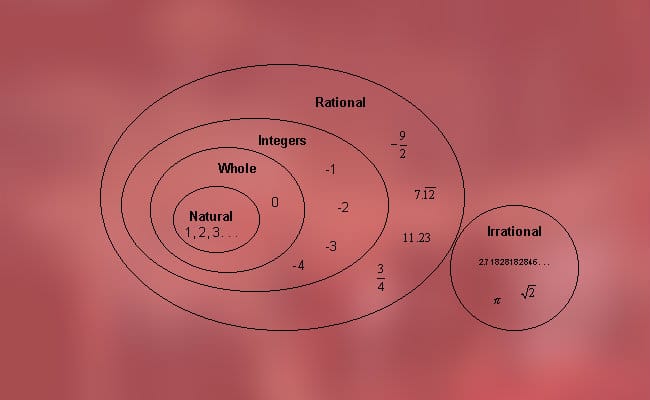
Эти числа можно разделить на два типа, о которых мы упоминали ранее, то есть рациональные числа (положительные, отрицательные и нулевые) и иррациональные (алгебраические и трансцендентные). Точнее можно найти следующую классификацию:

1. Рациональные числа

Это имя, данное числам, которые могут быть представлены как деление целых чисел или, что то же самое, обыкновенная и текущая дробь, в которой числитель и знаменатель не равны нулю и не меньше его.

Они, в свою очередь, также делятся на несколько типов: целые (натуральные, нулевые и отрицательные целые числа) и дробные (правильные и неправильные дроби).

а) Целые числа

Целые числа представляют собой набор натуральных чисел, отрицательных целых чисел и нуля, которые обозначаются буквой «Z». Целые числа также обычно представлены в числовой строке, где положительные или натуральные числа находятся справа, ноль - в середине, а отрицательные - слева.

• Считается "натуральные числа”Для тех, кто привык считать предметы или выполнять некоторые из наиболее распространенных и простых расчетных операций.
• El Cero Это нулевое значение, то есть в нем отсутствует значащая цифра, когда оно не сопровождается. Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет.
• отрицательные целые числа они используются противоположно положительным или естественным, то есть вместо того, чтобы считать, их использование состоит в том, чтобы вычитать, иметь, тратить или быть ниже. Чтобы их упомянуть, необходимо перед числом указать термин «минус», например «минус четыре».

б) Дробное

Также среди вещественных чисел можно найти этот тип в рациональных числах, которые возникли с целью решать задачи относительно деления натуральных чисел. Дробное число - это просто выражение, которое указывает деление одной величины на другую.

Дроби характеризуются числителем и знаменателем, которые отделены друг от друга диагональной или горизонтальной чертой. Однако, несмотря на то, что в целых числах мы также можем найти «простую дробь», в этом разделе типы дробей, которые мы находим, правильные и неправильные.

• Правильные состоят из тех, у которых числитель меньше знаменателя.
• Неподходящие будут наоборот, то есть знаменатель больше знаменателя.

2. Иррациональные числа

Иррациональные числа - это числа, которые нельзя записать в виде дроби, поскольку их десятичные дроби продолжают повторяться бесконечно. Например, невозможно записать дробь, включающую число Пи, е, соотношение золота и корней квадратные, кубические и другие.

Иррациональные числа возникли благодаря потребности ученика Пифагора записать корень в виде дроби; понимая, что это невозможно и что сегодня мы знаем это число под термином «иррациональное». Однако Пифагор не согласился с его открытием, хотя оно приписывается ему не меньше, чем его школе.

Кроме того, их можно разделить на два типа: алгебраические и трансцендентные.

• алгебраический те, которые позволяют решить алгебраическое уравнение.
• трансцендентный Это те, которые не могут быть представлены конечным числом корней (в отличие от алгебраических) и которые не следуют шаблону в своих десятичных дробях. Среди них находим число Пи.

Пока что мы подошли к классификации действительных чисел, которую, как мы надеемся, было легко читать и понимать; поскольку многие люди не любят математику, и мы сделали все возможное, чтобы дать подробное и простое объяснение.