Es una figura geométrica tridimensional que está compuesta por dos polígonos paralelos iguales como bases y caras laterales que son paralelogramos. Reciben un nombre específico según la cantidad de lados que formen su base. Así tenemos, por ejemplo, que si sus bases tienen tres lados será un prisma triangular, cuatro lados rectangulares, cinco lados pentagonales, etc.
El tema que nos ocupa es específicamente todo lo referente al prisma pentagonal, pero es necesario conocer los aspectos comunes a los prismas en general.
Características generales de un prisma
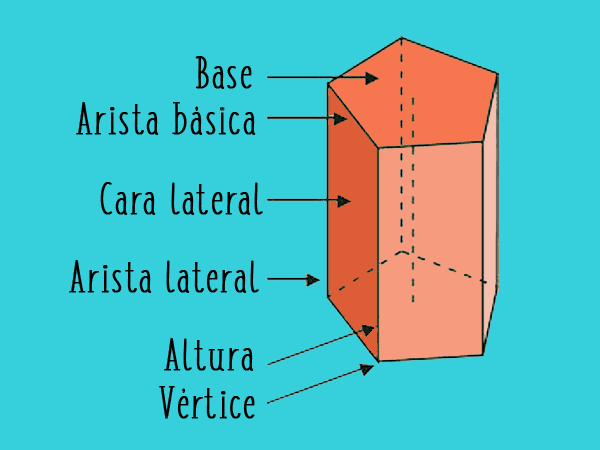
Elementos que conforman un prisma:
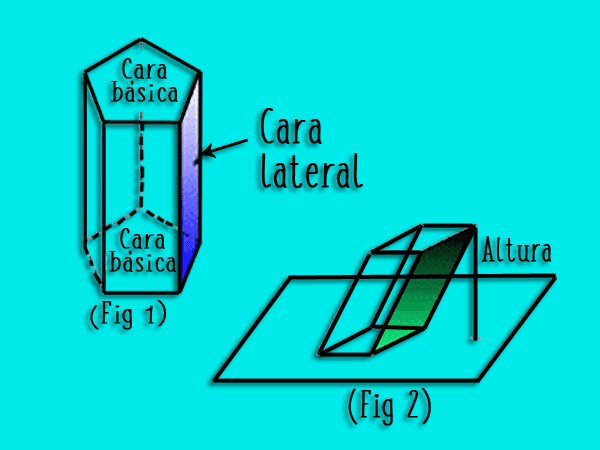
- Bases Son dos polígonos paralelos e iguales que forman el piso y la tapa del prisma. La cantidad de sus lados puede ser variable y son precisamente los que le dan nombre y apellido al prisma.
- Caras laterales: son los paralelogramos que separan la base inferior de la superior
- Altura: Es la distancia que se halla separando las dos bases.
- Aristas: Cada uno de los lados de los polígonos que forman las bases son llamados, aristas de la base. Y cada uno de los lados de las caras laterales de forma individual es llamado, arista lateral.
- Vértice: Cada una de las puntas donde se encuentran las aristas se llama vértice.
Clasificación de los prismas
Un prisma se clasifica según las propiedades de sus bases en:
- Regular:Es aquel cuya base es un polígono que tiene todos sus lados de igual longitud y también sus ángulos internos son de la misma medida.
- Irregular: Es aquel cuyas bases están representadas por polígonos de lados y ángulos internos diferentes entre sí
Según en el número de lados que tienen sus bases se clasifican en:
- Triangular 3 lados
- Cuadrangular 4 lados
- Pentagonal 5 lados
- Hexagonal 6 lados
- Heptagonal 7 lados
- Octogonal 8 lados
- Eneágono o nonágono 9 lados
- Decágono 10 lados…, y así sucesivamente.
Según sus caras laterales están clasificados en:
- Prisma recto: Es el que tiene tantas caras laterales como tenga su base, son rectangulares y paralelas a la misma.
- Oblicuos: Un prisma oblicuo no posee perpendicularidad en sus caras laterales con respecto a su base. Sus caras laterales son romboides. Tienen como característica particular que su altura no coincide con el valor de sus aristas laterales.
Según sus ángulos internos se clasifican en
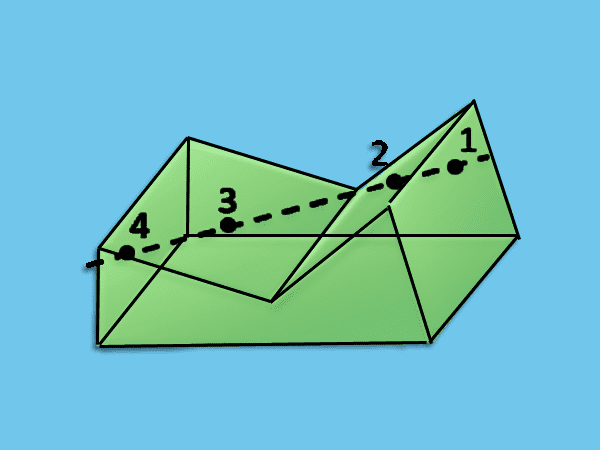
Cóncavos: Un prisma se puede clasificar como cóncavo cuando sus ángulos internos son mayores a 180°. Debido a su forma irregular, que da la visión de una hendidura hacia dentro del prisma, si lo atravesamos con una recta puede ser cortado en más de un punto.
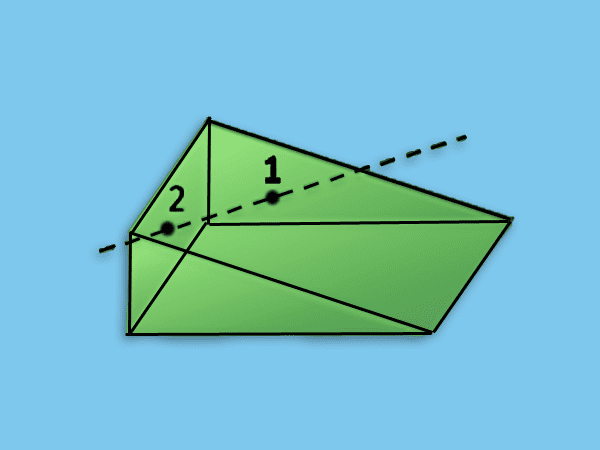
Convexos: Un prisma es convexo cuando sus ángulos internos miden menos de 180° y por otra parte tenemos que al atravesarlo con una recta solo se corta en dos únicos puntos.
Prisma pentagonal
Ahora sí, estamos listos para conocer más detalladamente al prisma pentagonal. Ya identificadas las características comunes a todo prisma, ahondaremos específicamente en el Prisma Pentagonal. Un prisma pentagonal es aquel cuyas bases son pentágonos iguales y paralelos y cinco paralelogramos que forman sus caras laterales.
Características
El prisma pentagonal posee las siguientes características:
- Bases. Tiene dos pentágonos paralelos e iguales.
- Caras. Presenta cinco caras laterales más las dos bases, en total son siete caras,
- Altura. Es la distancia comprendida entre las dos bases.
- Vértice. Son las puntas del prisma donde coinciden tres de las caras, en total son 10 vértices.
- Aristas. Son los puntos de encuentro de dos de las caras del prisma, en total tiene 15 aristas.
Según el Teorema de Euler existe una interrelación entre el número de caras (C), las aristas (A) y los vértices de todo prisma cuyos ángulos internos midan menos de 180° (convexos).
Aplicando la formula A=C+V-2 se puede hallar el número de aristas de un prisma pentagonal.: A=7+10-2= 15
Cómo calcular el área de un prisma pentagonal regular
Tiene sus bases de pentágonos regulares y lados rectangulares iguales, entonces el cálculo de su área está dado por:
Área= 5. L. (ap. + h), donde L es la medida de uno de los lados del pentágono, ap. (apotema) es la distancia más corta desde el centro a cualquiera de sus lados y h es la altura del prisma.
¿Cómo hallar el valor de ap (apotema) de un prisma pentagonal?
Es una variable que no conocemos tan evidentemente como las otras. Pues he aquí la fórmula matemática de hallarla.
Sabiendo el número de lados (N) y su medida (L), calcular en primer lugar el ángulo central que se forma entre el centro del polígono y dos vértices consecutivos, así:
? =360°/ N
Ejemplo: ángulo central de un pentágono ? = 360°/ 5 es igual a 72°.
Seguidamente se halla la apotema
Dividiendo la medida de uno de los lados (L) entre dos veces la tangente de la mitad del ángulo central (?)
ap = L / 2 x tang (? / 2)
Ejemplo: teniendo un prisma pentagonal cuyos lados tienen una medida de 20 cm y 30 centímetros de altura hallemos su área. Ya sabemos que el valor del ángulo central de un pentágono regular es de 72°. Hallemos su apotema:
Ap = 20 / 2 x Tang (72/2)
Ap = 20 / 2 x Tang (36)
Ap = 20 / 2 x (0.73)
Ap = 20 / 1.46
Ap = 13,69 cms.
Ahora sí, contamos con todos los datos para determinar su área:
Área= 5 x L x (ap + h)
5 x 20 (13,69 + 30)
100 (43,69)
Área = 4369 cm.
Área de un prisma pentagonal irregular
Tomando en cuenta que un prisma pentagonal irregular tiene como base dos pentágonos irregulares, es necesario hallar el área del pentágono irregular (Ab), su perímetro (Pb) y altura del prisma para luego calcular el área del prisma.
La fórmula del área de un prisma recto pentagonal irregular es:
Área del prisma = 2 . Ab + Pb . h
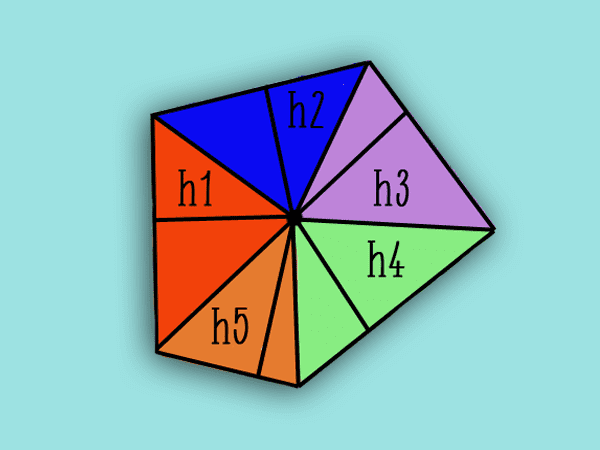
El área del pentágono irregular base (Ab) se halla mediante el método de triangulación, que significa dividirlo en figuras triangulares más pequeñas para calcular sus áreas y así más fácilmente se obtiene el área total del pentágono sumando todas ellas.
El perímetro de un pentágono irregular base (Pb) se halla sumando la medida de sus cinco lados.
Área de un prisma pentagonal oblicuo
La fórmula de cálculo de área para este tipo de prisma es diferente a la del prisma pentagonal recto.
El área de las bases se calcula de igual forma que en el recto, la diferencia radica en los laterales por el hecho de ser inclinados.
El área de uno de los laterales de un prisma pentagonal oblicuo se calcula en base a la medida de una arista lateral y el perímetro de la sección recta del prisma.
La intersección de un plano con el prisma a un ángulo de 90° con cada una de las aristas laterales, es la sección recta del prisma. Es decir, es la base plana que se observa al dividir transversalmente el prisma.
Para hallar la representación gráfica de la sección recta de un prisma oblicuo cualquiera, colocar la escuadra apoyada en una de sus aristas y formando un ángulo de 90° trazar una línea que llegue hasta la arista contigua y así sucesivamente con las otras aristas. Una vez hecho este procedimiento se puede visualizar en el plano esa superficie.
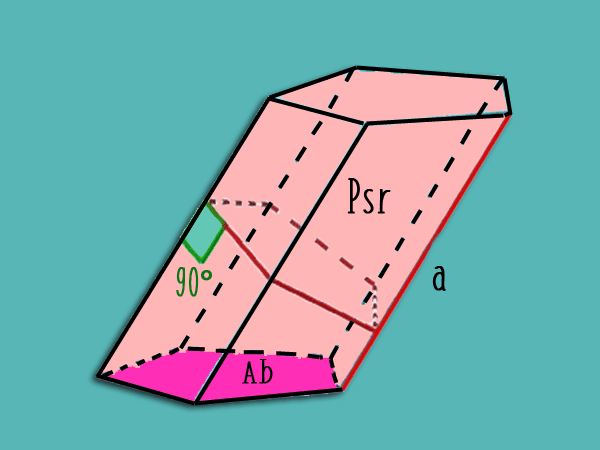
Área = 2 . Ab + Psr . a
Donde Ab es el área de la base, Psr es el perímetro de la sección recta del prisma y a una arista lateral.
Para determinar el valor del perímetro de la sección recta basta con hacer escuadra en una de sus aristas a un ángulo de 90° , medir la distancia que se forma desde esa arista hasta donde se intersecta con su arista paralela y sumarla cinco veces.
Volumen de un prisma pentagonal
Para calcular el volumen de un prisma pentagonal tanto recto como oblicuo se aplica la formula general para todo tipo de prisma: multiplicar el área de la base (Ab) por la medida de altura (h).
Volumen = Ab . h
Sustituyendo Ab por su fórmula propia tenemos que Volumen = 5. L . ap / 2 . h
Recordar que en un prisma recto la medida de altura es igual a la medida de la arista lateral mientras que en un prisma oblicuo la altura del prisma no coincide con la medida de la arista lateral, sea cual sea el tipo de prisma, atento a no confundir.
Cómo hacer un prisma pentagonal regular recto
? = 108° ángulo interno que se forma entre dos de los lados del pentágono base (medida fija para una figura pentagonal)
L = lado
H= altura
Trazo de la base pentagonal
Antes de comenzar a trazar el prisma se deben definir sus bases. De una manera fácil y no tan técnica te explicare como hacer una figura pentagonal regular.
- traza una línea recta que te servirá de base para comenzar( fig. 1)
- marca la medida que quieres darle a los lados de tu pentágono, línea (a-b) Fig. 2
- Con ayuda de un transportador, parándote en el punto “a “y hacia la izquierda busca el ángulo de 108°, traza una línea entre “a” y la intercesión con el ángulo hallado y sobre ella marca la medida elegida para los lados del pentágono. (línea a-c) fig.3
- Apóyate en el punto b y hacia la derecha hacer el mismo procedimiento anterior y hallar el otro lado (línea b-d) fig. 4
- Seguidamente apóyate en el punto “c”, siempre buscando un ángulo de 108° y trazar la ( línea c-e) fig.5
- Por último, unir los puntos e-d que conforman el lado que falta. Automáticamente debe tener el ángulo de 108°. Fig.6
Esta figura geométrica tiene formas más técnicas y precisas para su trazo, pero aquí te la explico de una manera sencilla utilizando solo reglas y/o escuadras y un transportador.
El éxito de la construcción de tu prisma dependerá de la exactitud en el trazo de sus bases.
Y la exactitud en la construcción de tu base pentagonal dependerá de tu habilidad y conocimiento de las herramientas de medición que te sugiero.
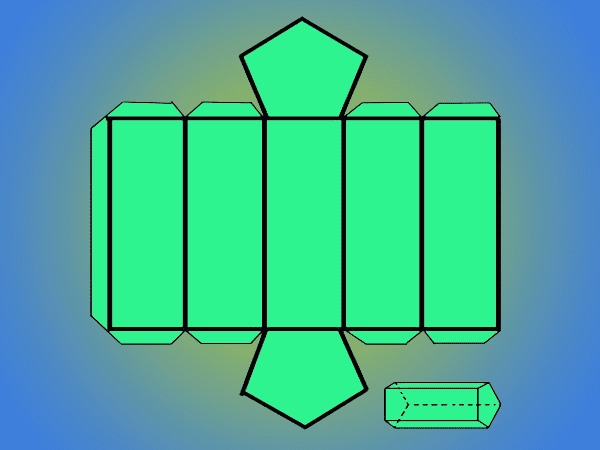
Trazo del prisma
- Trazar una línea recta larga que te servirá de base para comenzar el trazo.
- Sobre esa línea marca la medida (L) cinco veces una a continuación de la otra.
- Perpendicular a cada punto traza las líneas verticales que representan las aristas con la medida de (h) altura.
- Une todos los puntos con línea recta y te quedara un rectángulo dividido en cinco secciones iguales y paralelas, estos representan cada una de las caras laterales del prisma.
- En el rectángulo o cara central, o la de tu preferencia, dibuja o añade la base pentagonal tanto en la parte superior como en la inferior. Es necesario que la hagas primero y en base a ella traces el prisma.
- Añade pestañas por todos los lados de las caras laterales a excepción de una ellas. Estas pestañas son las que te servirán para armar el prisma.
- Recorta y aplica pegamento en las pestañas, remarca todas las líneas a fin de darle un poco de quiebre y tengas más facilidad para doblar las aristas.