Vamos a conocer todos los tipos de funciones matemáticas, algo esencial tanto para estudiantes como para los amantes de la rama científica, de manera que conseguirán una base imprescindible para poder seguir avanzando en sus conocimientos.
Qué son las funciones matemáticas
Una función es la relación existente entre dos conjuntos o magnitudes de manera que se establece una igualdad de valores entre el primero y el segundo.
Podemos representar una función de forma gráfica de manera que podremos observar la relación existente entre ambas magnitudes, lo cual facilita su entendimiento y sobre todo nos abre la mente para saber qué es lo que estamos calculando realmente.
Recordad que las matemáticas pueden ser muy bonitas pero tan sólo si entendemos los procesos y los objetivos, ya que, si no disponemos de una buena base y nos centramos tan sólo en el cálculo, al final se pueden acabar convirtiendo en una asignatura que se hace muy cuesta arriba. Así que es esencial que, además de calcular funciones, también dediquéis un tiempo a analizar su significado y, para ello, lo mejor que podéis hacer es representarlas gráficamente.
Todos los tipos de funciones matemáticas
Una vez que entendemos el concepto de función, podemos pasar a analizar todos los tipos de funciones matemáticas que existen en la actualidad.
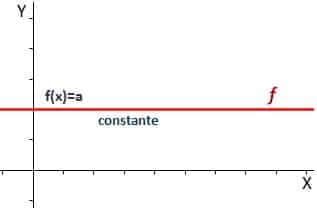
La función constante
Una función constante es aquella en la que tan sólo tenemos un resultado para dicha función, de manera que obtenemos algo similar a lo que podemos ver en la imagen siguiente, es decir, una recta horizontal:
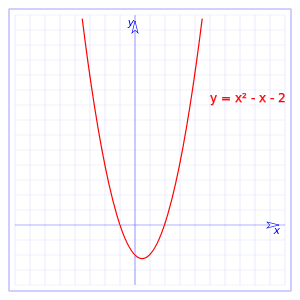
La función cuadrática
Una función cuadrática es una función del tipo f(x) = ax2 + bx + c, de manera que a, b y c serían las constantes siendo a en todo caso diferente de cero. De esta manera, lo que se obtiene es una parábola que puede estar abierta hacia arriba o hacia abajo, dependiendo de si a tiene un valor superior a cero, o si tiene un valor inferior a cero. En el caso de que sea un valor superior será abierta hacia arriba, y si es un valor inferior a cero, será abierta hacia abajo.
Cabe destacar que las funciones cuadráticas son funciones polinómicas.
La función lineal
La función lineal es aquella que tiene la forma f(x) = mx + b, donde m es lo que nos indica la pendiente, mientras que b es el valor en y, de manera que se obtiene una recta pero en esta ocasión con una inclinación o pendiente determinada.
Es importante tener en cuenta que una función lineal es una función polinómica, un tipo de función de la que vamos a conocer más a continuación.
La función polinómica
En cuanto a la función polinómica, se trata de una función con números reales y exponentes enteros positivos. Cabe destacar que el dominio de todas las funciones polinómicas es el conjunto de los números reales.
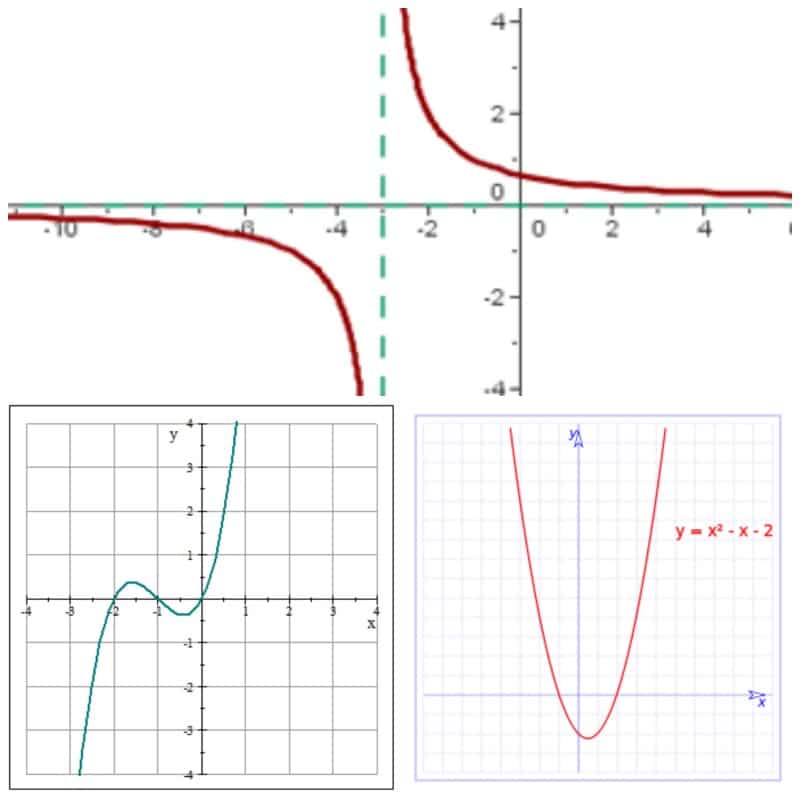
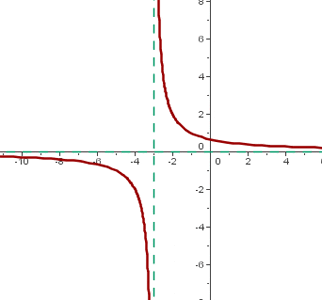
La función racional
Finalmente tenemos la función racional que es el cociente resultante de dos funciones polinómicas, de manera que se establece que q(x) = f(x) / g(x).
Un detalle a tener en cuenta es que el dominio de la función polinómica obtiene números reales.
La función de la recta
Cuando hablamos de la función afín, tenemos que mencionar que se trata de una función polinómica. Que también la hemos mencionado en este listado de funciones matemáticas. Por lo que volviendo a la afín, se define como la que no pasa por el origen de las coordinadas, es decir, que no toca el punto 0,0. Son rectas que se rigen por la siguiente fórmula:
F(x)=mx+n
La m será la pendiente, es decir, la inclinación con respeto al eje X o de abscisas. cuando es positiva se dice que la función es creciente. Por lo que si es negativa, será decreciente. La n será la ordenada, el punto donde la recta va a cortar el eje de coordenadas.
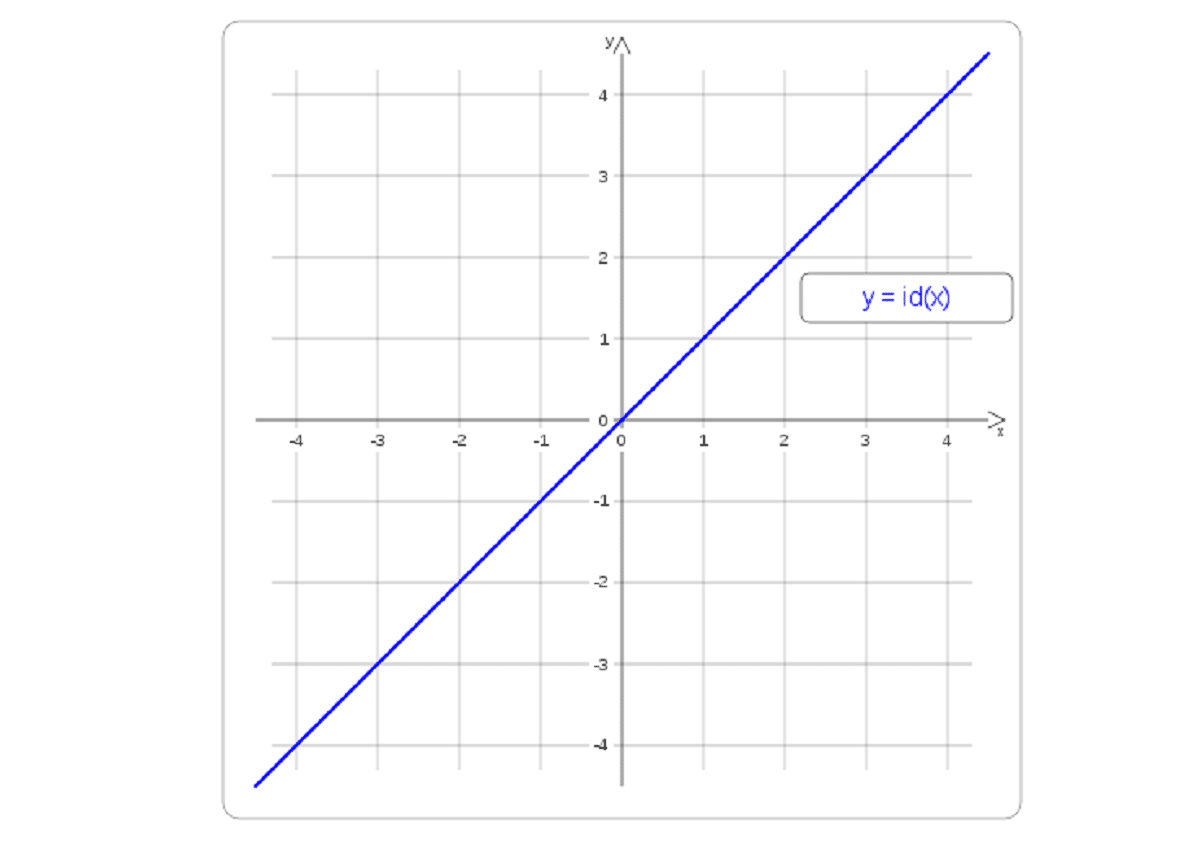
La función de identidad
Es la función de un conjunto a sí mismo. Es decir, que la imagen de cualquier tipo de elemento, será ese mismo. Solemos verla con id. Cuando hablamos de función de identidad también lo hacemos de una función lineal, donde m es igual a 1 y pasa por el eje de coordenadas. Esto hace que va a dividir tanto el primer como el tercer cuadrante y ambos, en partes iguales. Recuerda que id será siempre el elemento neutro
id r: R — R
id r (x): = x
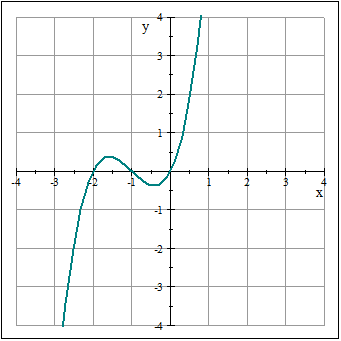
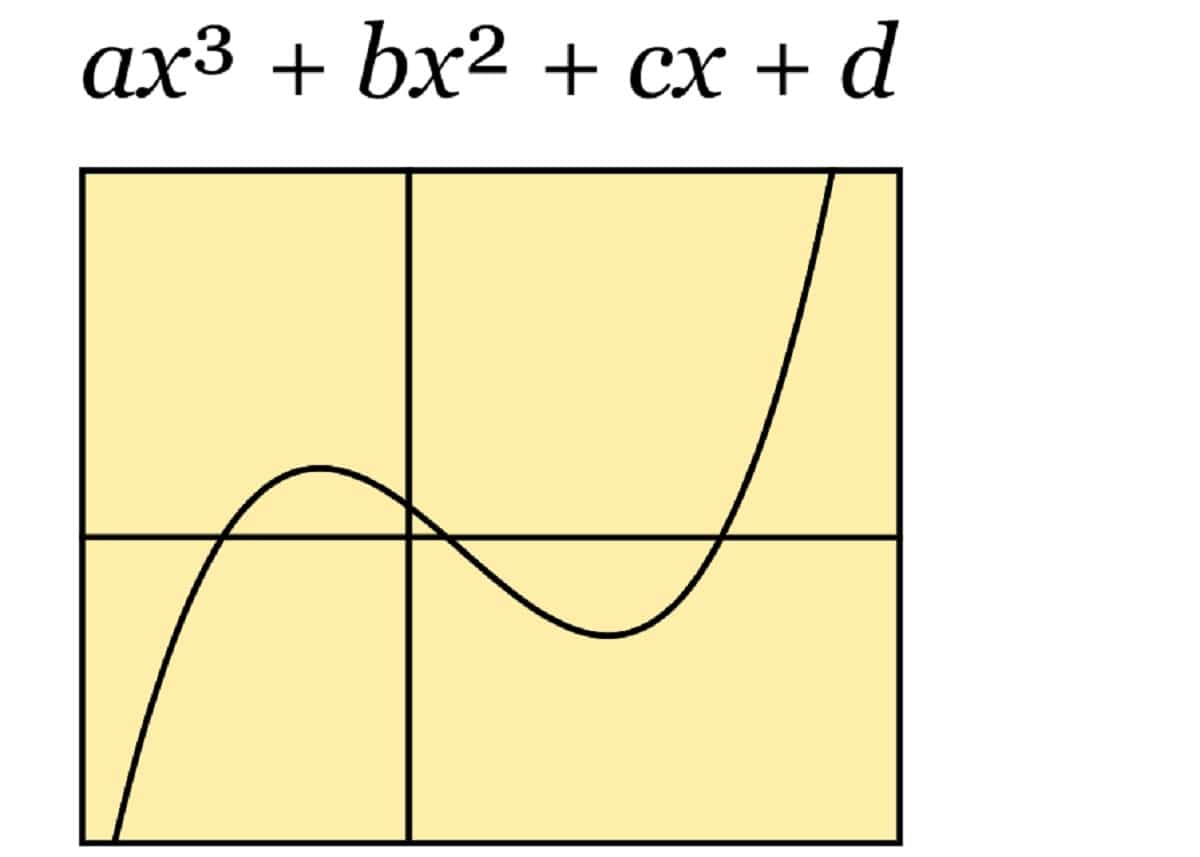
Función cúbica
Hablamos de funciones de tercer grado, donde el mayor exponente es x elevado a tres. Recuerda que a es distinta de cero. Puede contar también con una o varias raíces.
f(x)= ax 3 + bx 2 + cx + d
Función exponencial
En su base tiene una constante a y la variable x aparecerá como un exponente. La derivada de una función exponencial será proporcional al valor de la función. Por lo que la constante de esta proporcionalidad, será el logaritmo natural de la base b.
f(x) = ab×
Función logarítmica
Para hacernos una visión más rápida, hay que decir que es la inversa de la exponencial. por lo que cuando hablamos de las funciones logarítmicas, tenemos que mencionar que a será la base de dicha función, positiva y distinta de 1.
f (x) = logax
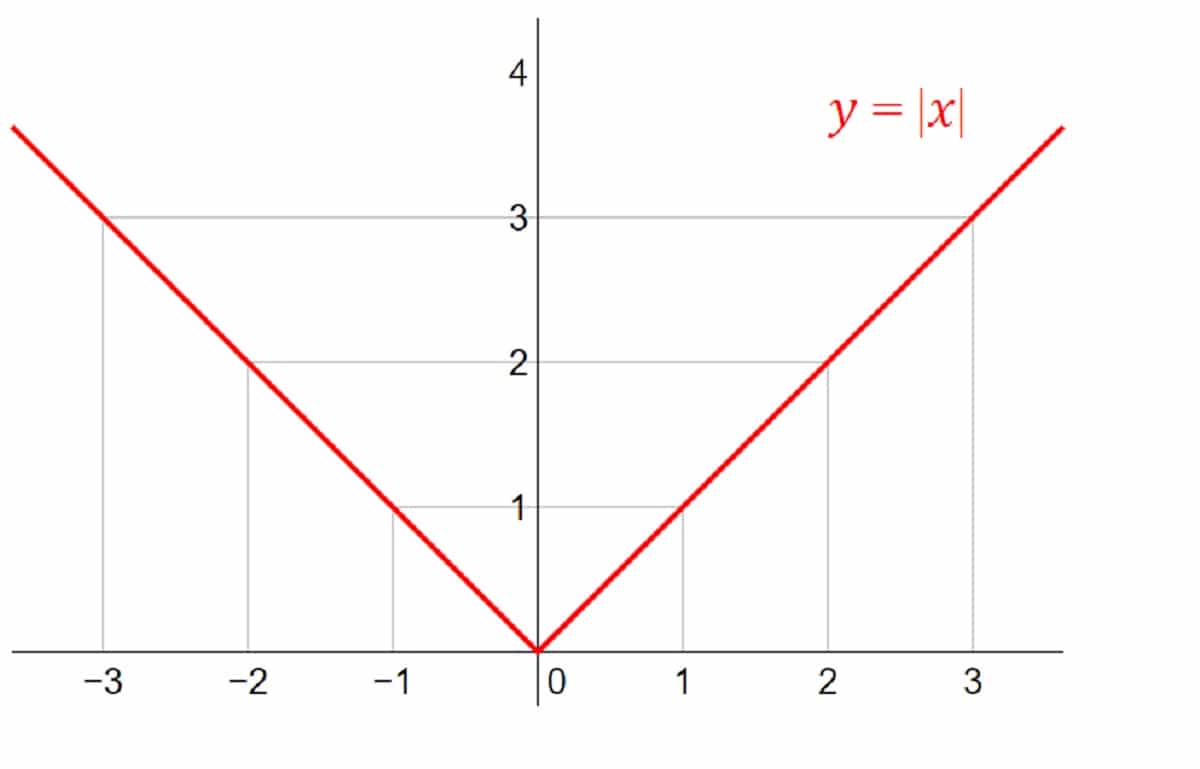
Función valor absoluto
Como seguro sabrás, el valor absoluto de un número en matemáticas es su valor numérico. En este caso no se tiene en cuenta si es positivo o negativo. En las funciones, se vincula con la magnitud o las distancias. La será mayor o igual que 0 pero nunca negativa.
f (x) = |x|
Con esto finalizamos la clasificación con los diez tipos de funciones matemáticas, una información que deberemos guardar para tener siempre a mano ya que es esencial que entendamos que, en base al tipo de función que tengamos delante, la representación gráfica variará considerablemente, de manera que, conociendo todos estos detalles, vamos a poder adelantar mucho trabajo ya que con un solo vistazo tendremos toda la información necesaria para saber cuál será el resultado y ya no nos quedará más que realizar el cálculo.
Tened en cuenta que vamos a conseguir mucho si ya de antemano sabemos el tipo de representación que nos vamos a encontrar, ya que esto nos va a ayudar en dos sentidos; en primer lugar podremos ir observando que todo vaya avanzando de forma correcta, es decir, deberemos tener claro que durante el proceso iremos viendo que vamos por un buen camino, y por otra parte, una vez que realicemos la representación gráfica, tendremos una idea clara acerca de si el resultado obtenido es el correcto, ya que en el caso de que la representación gráfica fuese diferente al tipo de función que estamos tratando, evidentemente querría decir que nos hemos confundido en algún cálculo, lo que significa que tenemos que volver otra vez hacia atrás hasta encontrar el error para subsanarlo y acabar comprobando que la representación gráfica es correcta.
Esto es todo lo que necesitáis saber acerca de los tipos de funciones, pero recordad que siempre es importante que ampliéis los conocimientos y sobre todo que practiquéis, entendiendo a la vez lo que estáis haciendo, puesto que es la única forma de poder disfrutar de las matemáticas y evitar que se conviertan en una asignatura a la que no conseguimos sacarle el lado bueno.
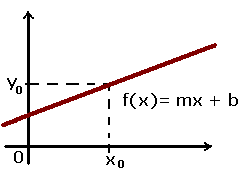
gracias por sus conocimientos brindados. me fue útil para la realización de mi trabajo pero si seria bueno que tuviera la fecha en la que realizo el trabajo y el nombre completo para tener presente la referencia bibliográfica y no hacer plagio.